Units: cm=centimeter, ft=foot, g=gram, gal=gallon (U.S.), GPa=GigaPascal, in=inch, kg=kilogram, km=kilometer, lb=pound, m=meter, min=minute, N=Newton, Pa=Pascal, s=second
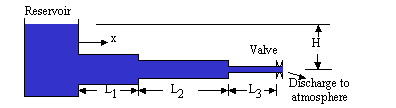
Water Hammer Diagram Piping Diagram (pipes do not have to be horizontal)
Topics: Introduction
Equations
Variables
Discussion
Fluid properties, Pipe properties, Minor loss coefficients, Pipe wall thickness
Error Messages
References
Introduction
Rapidly closing or opening a valve causes pressure transients in pipelines, known as water hammer or hydraulic transients. Valve closure can result in pressures well over the steady state values, while valve opening can cause seriously low pressures, possibly so low that the flowing liquid vaporizes inside the pipe. Our water hammer calculation computes the maximum and minimum piezometric pressures (relative to atmospheric) in each pipe in a pipeline as well as the time and location at which they occur. The hydraulic transient calculation is helpful in design to determine the maximum (or minimum) expected pressures due to valve closure or opening. If you are investigating the cause of pipe rupture, the software can provide insight as to what the pressure may have been in the pipeline during the rupture.
Our calculation simulates water hammer in a pipeline flowing full, bounded upstream by a large reservoir and bounded downstream by a valve which discharges to the atmosphere. The reservoir is assumed to be large enough to absorb changes in pressure and remain at the same elevation during the transient. There can be up to three pipes in series having different lengths and diameters but the same pipe material. The time to close (or open) the valve is entered. Also, the hydraulic transient program allows you to enter an intermediate time and % open so that the valve curve can be represented by two piece-wise linear equations, rather than a step function or single linear function. If the valve is being opened, you must also enter the minor loss coefficient (K) for the valve. Additional information can be found in Equations, Variables, and Discussion.
Equations
To Calculation
Mass conservation and momentum conservation are the fundamental equations used to analyze hydraulic transients (water hammer). The boundary conditions consist of a large reservoir at the upstream end of the pipeline and a valve at the downstream end discharging to the atmosphere. The equations, subject to the boundary conditions, are not readily solved analytically - a numerical solution is required. We used the method of characteristics to obtain a solution. The method of characteristics is a finite difference technique where pressures are computed along the pipe for each time step. Our software automatically sub-divides the pipe into sections (i.e. reaches or intervals) and selects a time interval for computations. Computational accuracy is enhanced by having lots of pipe sections and time steps; however, 2 or 3 digit accuracy is generally obtained in a pipe having as few as 5 sections while 6 digit accuracy is typically obtained with 50 sections. The number of pipe sections used is shown in the calculation next to the pipe number after the calculation runs. You can "force" the calculation to have more pipe sections by decreasing Tmax, the total calculation time. Our software uses 100,000 pipe sections times time steps, with a maximum of 1000 sections per pipe. The product 100,000 was selected to provide maximum accuracy and fast computations. The Courant stability criterion is used to determine the number of sub-sections versus time steps.
The following equations can be found in Chaudhry (1987), Fox (1989), Hwang and Houghtalen (1996), and Wylie and Streeter (1978).
Mass Conservation and Momentum Conservation (|V| is absolute value since velocity changes direction during the transient). Courant stability condition for method of characteristics solution.
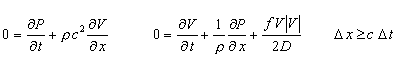
For each pipe:
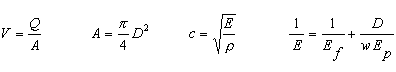
Boundary and Initial Conditions:
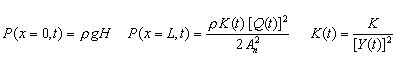
If valve initially closed: Q(x,t=0)=0. If valve initially open: Q(x,t=0)=Qmax
Valve closing or opening curves:
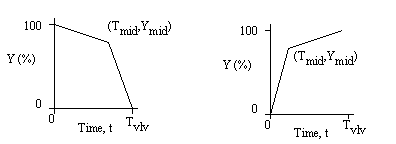
where Y(t) = 100 [K/K(t)]1/2. Our water hammer calculation allows you to enter the valve curve as two piecewise linear curves. See Discussion for further explanation.
Variables
To Calculation
Dimensions: F=Force, L=Length, M=Mass, T=Time
A = Pipe cross-sectional area [L2]. Up to three pipes can be used,
each with its own length and area. An = Area of the pipe furthest from the reservoir. Computed.
c = speed of pressure wave (celerity) [L/T]. Different for each pipe. Computed.
D = Diameter of each pipe [L]. Dn = Diameter of pipe furthest from reservoir. Entered.
E = Composite elastic modulus [F/L2]. Computed.
Ef = Elastic modulus of fluid [F/L2]. Computed.
Ep = Elastic modulus of pipe material [F/L2]. Computed.
f = Darcy-Weisbach friction factor (obtained from Moody diagram) for each pipe.
Computed automatically using same method as in
Design of Circular Liquid or Gas Pipes.
g = Acceleration due to gravity = 9.8066 m/s2.
h = Piezometric head in pipe (elevation + static head) [L] as a function of time and
distance relative to the valve elevation and relative to atmospheric pressure. Computed.
H = Head in reservoir relative to elevation of valve [L]. Vertical distance between
valve and reservoir surface. Entered.
K = Minor loss coefficient for valve when flow rate is Qmax. Entered if
valve being opened.
K(t) = Minor loss coefficient as a function of time while valve is being opened or closed. Computed.
L = Length of each pipe [L]. Ln = Length of last pipe (i.e. pipe furthest
from reservoir). Entered.
P = Piezometric pressure in pipe (elevation pressure + static pressure) [F/L2]
relative to the valve elevation and relative to atmospheric pressure. Function of
time and distance. Computed.
Pmin, Pmax = Minimum and maximum piezometric pressures in each pipe
[F/L2] relative to the valve elevation and relative to atmospheric pressure. Computed.
Q, Q(t) = Flow rate in pipe as a function of time [L3/T]. Computed.
Qmax = Steady state maximum flow rate in pipe [L3/T], when Y=100%. Entered.
t = Time [T].
Tmid = Intermediate time for user to enter Ymid. Tmid
must be between 0 and Tvlv. Entered.
Tvlv = Valve opening or closing time. Time to achieve Y=100% for opening
or Y=0 for closure. Entered.
Tmax = Maximum time for the calculation. Can be less than Tvlv.
Pmin and Pmax are found for each pipe in the time period up to Tmax.
V = Velocity in pipe as a function of time and distance [L/T]. Computed.
w = Wall thickness of each pipe [L]. Entered.
x = Distance along pipes measured from the reservoir [L].
Y, Y(t) = % that valve is open. 100% does not have to be a completely open valve,
but it is the most that the valve is open for the transient. See
Discussion for further information. Computed.
Ymid = % that the valve is open at Tmid. Entered.
Δt = Time Interval [T]. Computed.
Δx = Distance Interval [L]. Computed.
ρ = Fluid Density [M/L3].
μ = Fluid Dynamic Viscosity [F-T/L2].
ν = Fluid Kinematic Viscosity [L2/T]
= μ/ρ. Computed.
Discussion
To Calculation
Reservoir Elevation, H
Physically, the reservoir should have a large enough area such that H does not change
significantly during the transient. H is considered to be constant.
Composite Elastic Modulus, E
The equation shown above for E assumes that the pipe undergoes no longitudinal stress
(Hwang and Houghtalen, 1996, p. 121). Though this may not seem realistic due to the
liquid pulling on the pipe walls, very little difference in the value for E occurs in our
equation compared to more complicated equations (see References)
which account for expansion joints, fixed pipe ends, etc.
Pipes - Number and Orientation
You may enter up to 3 pipes in series. They do not have to be telescoping (e.g. pipe 2
can have a larger diameter than pipe 1), and they don't have to be horizontal. The
calculation is valid for horizontal and non-horizontal pipes. All pipes must be made
of the same material.
User can enter location to compute maximum and minimum pressure
Our calculation is set up to compute the overall Pmax and Pmin
for each pipe. However, say in the case of an actual pipe rupture, you may
need to know Pmax or Pmin at a specific location which may not
necessarily be where the overall Pmax or Pmin occurs. You can
do this by entering two pipes with the same diameter, with one of them being very
short. The two pipe lengths must add up to the actual pipe's length. Have the
short pipe located in the vicinity of the rupture.
Piezometric Head and Piezometric Pressure
Our calculation uses and computes piezometric heads and piezometric pressures. Even
though the calculation says "Min. Pressure in Pipe" and "Max. Pressure in
Pipe", these are piezometric pressures - not static pressures. (Due to space
considerations, the word "piezometric" was omitted from the headers.)
Head (h) has units of elevation (meters, feet). Pressure (P) has units such as
Pascal (N/m2), psi (lb/in2), or bars. We also allow pressure
to be output as meters of fluid or feet of fluid - which is actually a head rather than a
pressure. Pressure and head are related to each other by: P=ρgh (ρ
is the greek letter "rho" representing fluid density). Piezometric head =
elevation head + static pressure head. Piezometric pressure = elevation pressure +
static pressure. Static pressure is what people are usually referring to when they
ask, "What's the pressure in the pipe?" In our water hammer calculation,
the valve discharges to atmospheric pressure at an elevation of 0.0 m. Since the
valve discharges to atmospheric pressure, the static pressure at the discharge is 0.0 Pa
(we use pressures relative to atmospheric - also known as "gage pressure").
If your pipe is horizontal, then the elevation pressure and elevation
head are 0.0 everywhere in all pipes, and the pressures computed by the calculation are
the static pressures in the pipes. However, if the pipes are sloping, you need to
subtract off the elevation pressure from the computed piezometric pressure in order to
obtain static pressure. For example, let's say you run the calculation and the
maximum piezometric pressure in Pipe 1 is computed to be 166.3247 m at x=500 m. From
your pipe drawings, you know that this location is at an elevation of 50 m above the
valve. The static pressure head at x=500 m is thus: 166.3247 - 50 = 116.3247 m.
You can convert this to static pressure by (998.2 kg/m3)
(9.8066 m/s2)(116.3247 m)
(1 N-s2/kg-m)=1,138,696.5 N/m2
(assuming the fluid is water at 20oC
with a density of 998.2 kg/m3). Alternatively, instead of selecting
"Compute pressures in m of fluid", you could select "Compute pressures in
N/m2 or Pa". Then, the output maximum piezometric pressure in Pipe 1
is 1,628,144.2 Pa at x=500 m. Then the static pressure is computed as
1,628,144.2 N/m2 - (998.2 kg/m3)
(9.8066 m/s2)(50 m) = 1,138,696.8 N/m2,
which is the same (barring round-off error).
Pmax and Pmin at multiple locations along the
same pipe
Pmax or Pmin may occur at multiple locations along a pipe even
though the calculation only indicates one location. Usually this happens only when
the computed Pmax or Pmin has the same value as H (can be detected
if reservoir elevation and pressures have the same units). Splitting one pipe into
two pipes can provide additional values of Pmax and Pmin and their
locations for verification.
Discharge and Friction Factor
The valve is located at the end of the last pipe and discharges to the atmosphere.
The "steady Q at Y=100%" field that you enter is used to compute the initial
loss across the valve if the valve is initially open (i.e. if the valve is being closed)
and to compute the friction factor (f) for both the valve opening and closing
scenarios. Chaudhry (1987, p. 37) indicates that accuracy is sufficient if the
maximum steady state flow rate is used to compute f, rather than re-computing f every
distance and time increment as flow rate changes.
Valve
The valve minor loss coefficient (K) only needs to be entered if the valve is being
opened. If the valve is being closed, then the reservoir elevation (H), atmospheric
pressure boundary beyond the valve, and Qmax provide sufficient information to
compute pressures.
If the valve is only going to be opened half-way, enter K for a
half-open valve. If the valve will be opened completely, enter K for a fully open
valve.
To determine the valve curve: mathematically the valve curve is Y(t) =
100 [K/K(t)]1/2. However, physically it may be very difficult to
determine how K changes with time as the valve is opened or closed. A method for
computing K(t) is to run several steady state flow tests through the piping system with
different valve openings: measure pressure (P) just upstream of the valve and flow rate (Q)
for each valve setting. Then,

where A is the pipe area (not the flow area inside the valve).
If it is more convenient, using Y(t)=Av(t)/Av is an adequate
approximation for the valve curve - where Av is the valve area through which
water flows (not the pipe area). If finding Av(t) or K(t) is too
difficult, you can enter various valve curves and see if there is much difference in the
computed pressures.
Courant Stability Criterion
The Courant stability criterion shown in equations is a necessary
criterion for numerical solutions that vary in space and time, like the water hammer
calculation. Our program automatically satisfies this criterion. However,
satisfying the criterion can result in reducing the number of distance intervals
(sections) into which each each pipe is split. This can decrease accuracy.
There is a trade-off between time intervals and distance intervals with the product being
100,000, which we set to maximize accuracy while keeping the calculation fast. For 2
or 3 digit accuracy, try to have at least five pipe sections in each pipe (the number of
pipe sections is output next to the pipe number when the calculation is run). 50
sections gives about 6 digit accuracy. The hydraulic transient software will run if there are at
least 2 sections in each pipe. Reducing Tmax will increase the number of
pipe sections.
Fluid Properties, Pipe Properties, Minor Loss Coefficients, and Pipe Wall Thickness
To Calculation
Fluid Properties
Fluid density, viscosity, and elastic modulus provided by the drop-down menus in
the calculation, have been compiled from the closed conduit pipe flow references shown on
our literature web page.
Pipe Properties
Pipe material roughness, provided by the drop-down menus in the calculation, have been
compiled from the closed conduit pipe flow references shown on our literature web page. Pipe elastic moduli
have been compiled from the references shown below.
Minor Loss Coefficients References for K values
| Valve | Minor Loss Coefficient, K |
Valve | Minor Loss Coefficient, K |
| Globe, 100% open | 10 | Angle, 100% open | 5 |
| Gate, 100% open | 0.2 | Ball, 100% open | 0.05 |
| Gate, 75% open | 1.2 | Ball, 67% open | 5.5 |
| Gate, 50% open | 5.6 | Ball, 33% open | 210 |
| Gate, 25% open | 25 |
Pipe Wall Thickness (adapted from Glover, 1996)
Glover (1996) provides a fairly complete list of pipes and their wall thickness. The
tables below are a sampling adapted from Glover.
|
Plastic Pipe: PVC & CPVC Schedule 40 |
Plastic Pipe: PVC & CPVC Schedule 80 |
||||
| Nominal size (inch) | Actual inside diameter (inch) | Wall thickness (inch) | Nominal size (inch) | Actual inside diameter (inch) | Wall thickness (inch) |
| 0.5 | 0.622 | 0.109 | 0.5 | 0.546 | 0.147 |
| 1 | 1.049 | 0.133 | 1 | 0.957 | 0.179 |
| 2 | 2.067 | 0.154 | 2 | 1.939 | 0.218 |
| 4 | 4.026 | 0.237 | 4 | 3.826 | 0.337 |
| 8 | 7.981 | 0.322 | 8 | 7.625 | 0.500 |
| 12 | 11.938 | 0.406 | 12 | 11.376 | 0.687 |
|
Steel Pipe: Schedule 40 |
|||||
| Nominal size (inch) | Actual inside diameter (inch) | Wall thickness (inch) | Nominal size (inch) | Actual inside diameter (inch) | Wall thickness (inch) |
| 0.5 | 0.622 | 0.109 | 1 | 1.049 | 0.133 |
| 2 | 2.067 | 0.154 | 4 | 4.026 | 0.237 |
| 8 | 7.981 | 0.322 | 12 | 11.938 | 0.406 |
| 16 | 15.000 | 0.5 | 20 | 19.250 | 0.375 |
| 24 | 22.626 | 0.687 | 30 | 28.500 | 0.750 |
| 36 | 34.500 | 0.750 | 42 | 40.5 | 0.750 |
|
Copper Pipe: Type K |
Copper Pipe: Type L |
||||
| Nominal size (inch) | Actual inside diameter (inch) | Wall thickness (inch) | Nominal size (inch) | Actual inside diameter (inch) | Wall thickness (inch) |
| 0.5 | 0.527 | 0.049 | 0.5 | 0.545 | 0.040 |
| 1 | 0.995 | 0.065 | 1 | 1.025 | 0.050 |
| 2 | 1.959 | 0.083 | 2 | 1.985 | 0.070 |
| 4 | 3.857 | 0.134 | 4 | 3.905 | 0.110 |
| 8 | 7.583 | 0.271 | 8 | 7.725 | 0.200 |
| 12 | 11.315 | 0.405 | 12 | 11.565 | 0.280 |
Error Messages given by water hammer calculation
To Calculation
"Q, T's, Res, Moduli, Dens, Visc must be >0".
Flow rate, times, reservoir elevation, elastic moduli of pipe and fluid, fluid density, and
viscosity must be positive.
"K must be >0". Valve minor loss coefficient must be positive.
"Ymid must be: 0<Ymid<100%". The intermediate point on the
valve curve must be in this range.
"Tmid must be: 0<Tmid<Tvlv". The intermediate time on the
valve curve must be greater than 0 but less than the valve opening (or closure) time.
"Pipe 1: L, D, Wall Thick must be >0". Pipe length, diameter,
and wall thickness must be positive.
"Pipe 2: L, D, Wall Thick must be >0". Same as above.
"Pipe 3: L, D, Wall Thick must be >0". Same as above.
"Tmax must be >1e-10 sec". Pressures must be computed for
greater than 10-10 sec.
"Re or e/D out of range". Friction factor (f) can only be
computed if Reynolds number and roughness/diameter ratio are in the
range of the Moody diagram.
"Reduce Tmax". Tmax (maximum time for computation of
pressures) must be reduced in order to have sufficient distance sections (i.e. intervals,
reaches). There is a trade-off between time intervals and distance intervals with
the product being 100,000. In all cases, the program will be sure that the
Courant stability condition is satisfied. For decent accuracy,
try to have at least five pipe sections in each pipe (the number of pipe sections is
output next to the pipe number when the calculation is run). The calculation will
run if there are at least 2 sections in each pipe. If there are less than 2 sections
per pipe, the message will be displayed.
"Tmax too low". This message rarely occurs but has to do with the
precision of the calculation. We use double precision (the most precise) but
idiosyncrasies can still occur. Increase Tmax to eliminate this
message.
"Reservoir elev too low". The reservoir elevation is too
low for the flow and valve settings to be physically achievable.
"Warning: Pmin<Patm/2". At least one of the computed minimum
pressures is less than half of atmospheric pressure (-101325/2 N/m2 gage). The
equations used in the calculation don't care if pressure drops below 0.0 absolute, even
though in reality such pressures can never occur. The warning message indicates that the
results are not accurate below about half of atmospheric pressure. Note that Pmin
and Pmax are gage pressures (relative to atmospheric pressure).
References
To Calculation
Chaudhry, M. Hanif. 1987. Applied hydraulic transients. Van Nostrand Reinhold Co. 2ed.
Fox, J. A. 1989. Transient flow in pipes, open channels and sewers. John Wiley and Sons.
Glover, T. J. 1996. Pocket Ref. Sequoia Publishing Inc. 2ed.
Hwang, Ned H .C. and Robert J. Houghtalen. 1996. Fundamentals of hydraulic engineering systems. Prentice Hall.
LMNO Engineering, Research, and Software. 2009. Newsletter comparing water hammer calculations.
Wylie, E. Benjamin and Victor L. Streeter. 1978. Fluid transients. McGraw-Hill International Book Co.
© 2000-2025 LMNO Engineering, Research, and Software, Ltd. All rights reserved.
LMNO Engineering, Research, and Software, Ltd.
7860 Angel Ridge Rd. Athens, Ohio 45701 USA Phone: (740) 707‑2614
LMNO@LMNOeng.com
https://www.LMNOeng.com
