Liquid in cylindrical pipe or tank on an incline (tipped, slanted, sloped, leaning). Enter cylinder angle of inclination, length, diameter, depth, dipstick location. Graph, Table
Register to enable "Calculate" button. Demonstration mode for ∅=15o and D=2 m (cookies must be enabled).
Units in inclined cylinder calculation: barrel=42 gallons (US), cm=centimeter, ft=foot, gallon=gallon (US), m=meter
Topics: Introduction Discussion Equations Variables Messages
Introduction
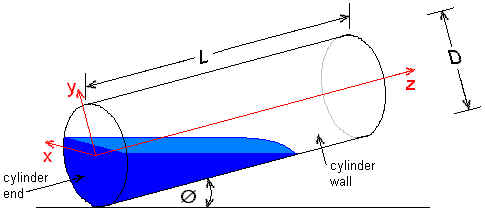
LMNO Engineering's inclined cylinder calculation computes the volume of liquid in a
partially full cylindrical container that is tipped, tilted, slanted, sloped, or leaning (all have the same meaning as inclined). The calculation is helpful for computing the volume
in a capped or clogged water pipe that is sloping downhill or a tank that is tipped,
sloped, or tilted. The volume can be multiplied by the liquid density in order to
determine the mass of liquid. The following sections present the method, equations, and
formulas used in the inclined cylinder calculation.
Discussion
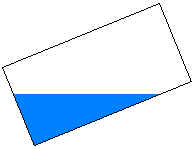
The bottom of the sloping cylinder is the downhill flat end, while the top of the sloping cylinder is the
uphill flat end. A coordinate system is assigned to the inclined cylinder, with the origin at
the center of the inclined cylinder bottom. The x-axis is perpendicular to and into the page,
the y-axis runs along the slanted cylinder bottom (in the plane of the page), and the z-axis is
the axis of the slanted cylinder.
"Depth measurement method"
The program allows three methods for measuring the liquid depth in the tipped cylinder. For
the first two methods, a dipstick (or sensor, or other measuring device) is inserted
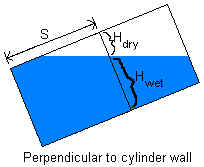
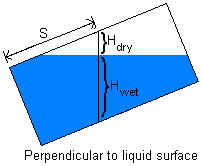
through the cylinder wall at a distance S from the bottom of the sloped cylinder. The
measurement can be either perpendicular to the inclined cylinder wall or perpendicular to the
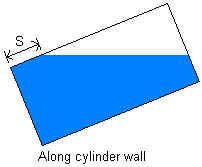
liquid surface. The third measurement method is "Along cylinder
wall". For this method, it is assumed that the bottom is completely covered. The
liquid level is determined, either visually or by using a sensor, as the intersection of
the liquid surface with the upper cylinder wall. The program does not allow liquid
level to be determined by a measurement from the ends of the sloped cylinder.
"Depth measurement type"
If a dipstick (or other device) is used to determine liquid level, the measurement
recorded is either the distance from the upper cylinder wall to the liquid surface (dry
depth) or the distance from the liquid surface to the lower cylinder wall (wet depth). If
the measurement method is "Along cylinder wall", then no measurement type is
needed.
"Minimum/Maximum volume"
For most situations, the minimum and maximum volume will be the same. The minimum and
maximum will be different in the following situations.
If the measured liquid depth is found to be zero, it is possible that there is actually some liquid in the slanted cylinder that the measuring device can't register. The calculated volume for the measurement is a maximum value. Since it is possible that the slanted cylinder is indeed empty, the minimum volume is zero.
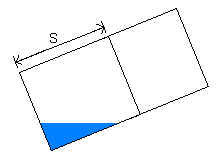
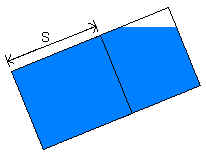
If the measurement indicates that the sloped cylinder is full, that doesn't necessarily mean that it is. There could still be some gas at the top of the inclined cylinder that the measuring device can't register. The calculated volume for the measurement is a minimum value. Since it is possible that the tilted cylinder is indeed full, the maximum volume is πr2L.
Equations for Inclined Cylinder
In performing the volume computation, a certain group of variables appears many times, so
they are grouped together and named "G".
For the situation in which the wet or dry depth is measured perpendicular
to the inclined cylinder wall:
G = S + (r-Hdry)/tan∅
For the situation in which the wet or dry depth is measured perpendicular
to the liquid surface:
G = S + r/tan∅ - Hdry/sin∅
For the situation in which the measurement is done along the sloped cylinder
wall:
G = S + r/tan∅
The liquid in the inclined cylinder is the volume bounded by the four surfaces:
1. The liquid surface, defined by the plane z =
y/tan∅ + G
2. The cylinder wall, defined by x2
+ y2 = r2
3. The bottom end of the cylinder, defined by
the plane z = 0
4. The top end of the cylinder, defined by the
plane z = L
If ∅ is large enough and the tilted cylinder is not very full, then the sloped cylinder top end will be dry and the volume is bounded by only the first three surfaces.
Depending on the dimensions and incline of the cylinder and the amount of liquid in it, the inclined cylinder bottom end can be completely or partially covered, and the inclined cylinder top end can be dry or partially covered. For cases in which the bottom end is partially covered, the liquid surface and the slanted cylinder bottom end intersect in the line y=-Gtan∅. For cases in which the top is partially covered, the liquid surface and the inclined cylinder top end intersect in the line y=(L-G)tan∅.
The general equation for calculating volume is:
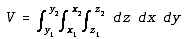
where x, y, z refer to the coordinate system. For all cases,
and
because the boundary of the liquid in the x-direction is defined by the inclined cylinder wall.
Also for all cases, z1=0. For cases in which the tipped cylinder top end is
partially covered, the integral must be broken into two parts - one which has the liquid
surface as its upper limit, and one which has the inclined cylinder top end as its upper
limit. The y-coordinate of the boundary between the two regions is given by
y=(L-G)tan∅. For cases in which the bottom end is completely covered, y1=-r. If
the bottom end is partially covered, then y1=-Gtan∅.
Case 1 - Bottom end covered, top end dry
Since the top end is dry, the volume is bounded in the upper z-direction by the liquid
surface. The equation is:
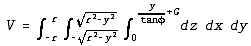
This turns out to be a fairly simple integral, with the solution V = πr2G. For
the special case where ∅=π/2, the cylinder is vertical and the solution reduces to V =
πr2S.
Case 2 - Bottom end partially covered, top end dry
Since the top end is dry, the volume is bounded in the upper z-direction by the liquid
surface. Since the bottom end is partially covered, y1=-Gtan∅. The
equation is:
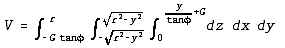
Case 3 - Bottom end covered, top end partially covered
Since the top end is partially covered, the integral is split into two parts. The
first part has the liquid surface as its upper limit, while the second part is limited by
the slanted cylinder top end. The equation is:
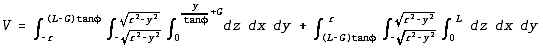
Case 4 - Bottom and top ends partially covered
The equation is:
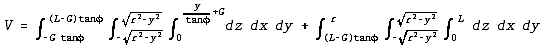
For the special case where ∅ = 0, the solution to this equation reduces to that of the
horizontal cylinder.
Variables for Inclined Cylinder
To use the equations above, a consistent set of units must be used. The variables below
show the SI (System International) units for each variable. Our calculation allows a
variety of other units with the conversions made internally within the program.
dx = Integral differential in x-direction (m).
dy = Integral differential in y-direction (m).
dz = Integral differential in z-direction (m).
D = Diameter of cylinder (m).
G = Collection of terms (m).
Hdry = Distance from upper cylinder wall to liquid surface = dry depth (m).
Hwet = Distance from liquid surface to lower cylinder wall = wet depth (m).
L = Length of cylinder (m).
r = Radius of cylinder = D/2 (m).
S = Distance along cylinder from cylinder bottom end to measurement location (m). If using
a dipstick, this is the location where the dipstick is inserted.
x = Coordinate shown in figure at top of page (m).
V = Liquid volume in inclined cylinder (m3).
x1 = Lower limit of x (m).
x2 = Upper limit of x (m).
y = Coordinate shown in figure at top of page (m).
z = Coordinate shown in figure at top of page (m).
∅ = Acute angle between lower cylinder wall and level ground (radians).
π = 3.1415926....
Messages given by Inclined Cylinder Calculation
"Dimensions must be >0", "Must have 0 ≤ S ≤ L",
"Need 0.01< ∅ <90 degrees". These are initial checks of input
data.
"Invalid dry or wet depth". Either dry depth or wet depth is input; the other is computed. This message appears if the input value is invalid or if the input value causes the computed value to be invalid. An invalid value is one that is either negative or which causes the sum of the wet and dry depths to exceed the dimensions of the cylinder.
"Meas. type must be wet or dry". This message appears if depth measurement type was set to "Not needed" and depth measurement method is not "Along cylinder wall". Either dry depth or wet depth must be input if depth measurement method is not "Along cylinder wall".
© 2006-2024 LMNO Engineering, Research, and
Software, Ltd. All rights reserved.
Please contact us for consulting or questions about inclined cylinder liquid volumes.
LMNO Engineering, Research, and Software, Ltd.
7860 Angel Ridge Rd. Athens, Ohio 45701 USA Phone: (740) 707-2614
LMNO@LMNOeng.com https://www.LMNOeng.com
LMNO Engineering home page (more calculations)