LMNO Engineering newsletters
2012
July 24, 2012. Drag Force
April 10, 2012. Energy Grade Line and Hydraulic Grade Line
January 12, 2012. Flow and Pressure
2010
November 22, 2010. Inverted Siphons
September 14, 2010. Gas Flow
February 10, 2010. Time to Empty a Tank
2009
December 1, 2009. Critical Depth in Circular Pipe
November 3, 2009. Instantaneous Valve Closure - Compare
two programs
October 6, 2009. Instantaneous Valve Closure - Water
Hammer
August 27, 2009. Hydraulic Jump
2008
May 29, 2008. Videos of Experiment and Analysis of
Water Discharging from a Tank
February 14, 2008. Fire Hydrant Pressure Requirement
2007
November 13, 2007. Summary of Software
2006
October 23, 2006. End Depth Method for Flow
Measurement in Open Channels
August 21, 2006. Volume in Inclined Cylinder
May 16, 2006. Gas Flow Conversions
April 4, 2006. Culvert Design
February 9, 2006. Newsletter Topics
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, OH 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. July 24, 2012
Drag Force
Drag force is caused by a fluid (such as water or air; or any liquid or gas) impinging
upon an object. An example is a rain droplet falling through air. Using the droplet as the
frame of reference, atmospheric air is impinging upon the water droplet. The drag force is
a function of the velocity and the impinging fluid's density (in this case, air) along
with the object's reference area and drag coefficient. The drag coefficient may further be
a function of the Reynolds number. Reynolds number depends on the impinging fluid's
density, viscosity, and velocity as well as the object's characteristic length.
Drag Force Equation:
F = 0.5 C d A V2
Using SI units (kg=kilogram, m=meter, N=Newton, s=second):
A = Reference area, m2.
C = Drag coefficient, dimensionless.
F = Drag force, N.
V = Velocity, m/s.
d = Density of impinging fluid (liquid or gas), kg/m3.
As an example, if a 0.1 m x 0.1 m x 0.1 m cube is completely submerged in a river with one
of its faces directly facing the 2 m/s velocity of river water, then:
A = (0.1 m)(0.1 m) = 0.01 m2
V = 2 m/s
d = 998.2 kg/m3 (at 20oC for water)
C = 1.05 from https://www.LMNOeng.com/Drag
Therefore:
F = 0.5 C d A V2
= (0.5)(1.05)(998.2 kg/m3)(0.01 m2)(2 m/s)2
= 20.96 N or 4.71 lb.
Thank you for your interest in the LMNO Engineering newsletter and the fluid flow
calculations website https://www.LMNOeng.com,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com.
(c) 2012 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, OH 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. April 10, 2012
Energy Grade Line and Hydraulic Grade Line
Two concepts that confound many students of hydraulics are EGL and HGL - Energy Grade Line
and Hydraulic Grade Line. Simply put, these are graphs of total head and hydraulic head
versus location along a pipeline.
Total Head (TH) is the sum of three terms: Elevation head + Pressure head + Velocity head.
Hydraulic Head (HH) is the sum of two terms: Elevation head + Pressure head.
Hydraulic Head is also known as Piezometric head.
Head is a fluid's energy per unit weight, having units of meters or feet.
If a pipe flow system has head losses (due to friction between the pipe walls and the
fluid, and due to valves, bends, contractions, expansions etc.), then TH decreases. If a
piping system contains a pump, then TH will increase across the pump. Note that:
TH1 + Pump Head = TH2 + Losses, so that TH2 can be computed as:
TH2 = TH1 + Pump Head - Losses
And for Hydraulic Head:
HH2 = TH2 - Velocity Head at 2 = TH1 + Pump Head - Losses - Velocity Head at 2
where location 1 is upstream of location 2.
Thank you for your interest in the LMNO Engineering newsletter and the fluid flow
calculations website https://www.LMNOeng.com ,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to
LMNO@LMNOeng.com .
(c) 2012 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, Ohio 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. January 12, 2012
Flow and Pressure
We receive many inquiries similar to, "What is the flow rate through a 6 inch
diameter horizontal pipe carrying water at 20 oC at a pressure of 100
psi?" This question is impossible to answer. Flow rate depends on a pressure
difference. If the person had said, "... pressure difference of 100 psi", then I
could answer the question. A common misunderstanding is that if pressure is known at one
point in a pipe, then flow rate can be determined - since somehow flow rate is related to
pressure. The fact is that flow rate is related to pressure difference.
Let's look at the energy equation for pipe flow from location 1 to location 2, which are a
length "L" apart. The constant diameter pipe carries an incompressible steadily
flowing fluid. Also, let's say there are no pumps or minor losses (valves, pipe bends,
etc.) between points 1 and 2. The velocities at 1 and 2 are the same since the flow is
steady, the fluid is incompressible, and the diameters are the same. The governing
equation reduces to:
(P1-P2)/S = H
where P1=upstream pressure [F/L2], P2=downstream pressure
[F/L2],
S=weight density of fluid [F/L3], H=major loss (also called friction loss) [L].
Note that S=dg where d=fluid density [M/L3] and g=acceleration due to gravity
[L/T2]. Units: [F]=Force, [L]=Length, [M]=Mass, [T]=Time.
H is a function of velocity, pipe roughness, diameter, and length. It is commonly
represented by the Darcy-Weisbach friction loss equation ( https://www.LMNOeng.com/pipe-flow-calculator.php
) or the Hazen-Williams friction loss equation ( https://www.LMNOeng.com/HazenWilliamsDesign.php
). After computing (P1-P2)/S, then velocity (and flow rate) can be
found using your preferred friction loss equation.
Please let me know if you have questions. Thank you for your interest in the LMNO
Engineering newsletter,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com .
(c) 2012 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, Ohio 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. November 22, 2010
Inverted Siphons (Depressed Sewers)
https://www.LMNOeng.com/Channels/InvertedSiphon.php
Stormwater and wastewater sewers often encounter obstructions such as rivers, other pipes,
subways, tunnels, or valleys. To pass these obstructions, a common method is for the sewer
pipe to drop sharply, then run horizontal under the obstruction, and finally rise to the
desired elevation. The piping going under the obstruction is traditionally called an
"inverted siphon" or "depressed sewer".
Unlike the main sewer pipe, the depressed sewer pipe(s) flow under pressure. Special care
must be taken in inverted siphon design since losses are greater for pressurized flow, and
the velocity in the depressed sewer should be at least 4 ft/s (1.2 m/s) for storm water or
3 ft/s (0.9 m/s) for sewage (Metcalf and Eddy, 1981) to keep sediment in suspension.
Therefore, even if there is only one main sewer pipe, several depressed pipes may be
required.
Our calculation at https://www.LMNOeng.com/Channels/InvertedSiphon.php
will determine the diameters of up to 5 siphons (design mode). The calculation will also
work in reverse (analysis mode) where you enter the siphon diameters, and the software
computes the flow rate through each siphon.
Whether running the calculation in design or analysis mode, the user enters the diameter,
slope, and Manning roughness coefficient for the main sewer pipe. The calculation computes
the discharge through the main sewer under design conditions (flowing full) using the
Manning equation. The user also enters the elevation difference between the inlet and
outlet junction chambers. The junction chambers are where the main sewer pipe branches
into the siphon pipes and where the siphon pipes then merge back into the main sewer pipe
after passing the obstruction. Additionally, the siphon length and Manning roughness
coefficient for the siphon pipes are entered since they may be of different material than
the sewer main.
Please let me know if you have questions about inverted siphons or other hydraulics,
hydrology, or fluid mechanics topics. Thank you for your interest in the LMNO Engineering
newsletter,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
Reference:
Metcalf and Eddy, Inc. 1981. G. Tchobanoglous, editor. Wastewater Engineering: Collection
and Pumping of Wastewater. McGraw-Hill, Inc.
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com.
(c) 2010 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, Ohio 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. September 14, 2010
Gas Flow (nomenclature at end of newsletter)
There are many issues to consider when using equations to predict gas flow in a pipe. If
the Mach number is low enough (M<0.3), then the gas can be modeled as an incompressible
fluid (Munson et al., 1998, p. 712) using https://www.LMNOeng.com/pipe-flow-calculator.php.
If the Mach number is greater than 0.3, then compressible equations should be used. Note
that M=V/c.
Unlike incompressible flow where density is constant along a pipeline, for compressible
flow, density varies. The mass flow rate is: W=dVA.
Subsituting the equation of state, d=P/(zRT), mass flow rate can be expressed as:
W=(PVA)/(zRT) (equation 1)
For steady flow in a constant-diameter pipeline, there are three fundamentally different
types of flow that can occur which have relatively simple methods for simulation. They are
isothermal flow, Fanno flow, and Rayleigh flow.
In isothermal flow, the temperature of the gas is constant along the length of the pipe.
Per equation (1), if W, A, z, R, and T are constant while pressure decreases due to
friction, then velocity increases along the pipeline. Isothermal flow can be modeled using
equations at https://www.LMNOeng.com/Flow/weymouth.php.
In Fanno flow, the pipe is fully insulated (no heat transfer). If flow is subsonic
(M<1), then pressure and temperature decrease with distance and velocity increases.
Fanno flow is commonly used to simulate gas flow in tubes and pipes where temperature is
known to change significantly.
In Rayleigh flow the pipeline is externally heated or cooled, but friction is assumed to
be negligible. Heating the gas results in increasing velocity as the gas travels down the
pipeline. External cooling results in lower velocity as the gas travels.
Nomenclature (SI units):
kg=kilogram, K=Kelvin, N=Newton, m=meter, s=second.
A=pipe cross-sectional area (m2), c=speed of sound (m/s), d=gas mass density
(kg/m3), M=Mach number, P=gas absolute pressure (N/m2), R=gas
constant (N-m/kg-K), T=gas absolute temperature (K), V=gas velocity (m/s), W=gas mass flow
rate (kg/s), z=gas compressibility factor (z=1 if ideal gas).
Reference:
Munson, B. R., D. F. Young, and T. H. Okiishi. 1998. Fundamentals of Fluid Mechanics. John
Wiley and Sons, Inc. 3ed.
Thank you for your interest in the LMNO Engineering newsletter,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com.
(c) 2010 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, Ohio 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. February 10, 2010
Time to Empty a Tank
https://www.LMNOeng.com/Tank/TankTime.php
We are sometimes asked how long it will take to empty a tank or drain a pond. We have had
a steady state program on our site for many years which computes flowrate as a function of
geometry and head or trajectory - https://www.LMNOeng.com/TankDischarge.php.
We now have a new calculation to compute the time for the liquid level in a tank to drop -
https://www.LMNOeng.com/Tank/TankTime.php.
The calculation uses the equation:
t = A/(a C) (Hi0.5 - Hf0.5) (2/g)0.5
where (sample units are shown in parentheses):
a = Orifice area (m2).
A = Tank cross-sectional area (looking down on the tank, m2).
C = Orifice discharge coefficient.
g = Acceleration due to gravity (9.8066 m/s2).
Hi = Initial liquid depth above orifice centerline (m).
Hf = Final liquid depth above orifice centerline (m).
t = Time for liquid to drop from Hi to Hf (sec).
For instance, if C=0.6, Orifice diameter=0.01 m, Tank diameter=0.5 m, Hi=3 m, Hf=0.2
m, then:
a = π d2 /4 = pi (0.01m)2 /4 = 7.854e-5 m2
A = π D2 /4 = pi (0.5m)2 /4 = 0.1963 m2
t = (0.1963 m2) / [(7.854e-5 m2)(0.6)] [(3
m)0.5 - (0.2 m)0.5] (2/9.8066 m/s2)0.5
= 2417 sec = 40.3 minutes
Instead of time, the calculation can compute one of the other variables - orifice
coefficient, initial depth, final depth, tank area (or diameter), or orifice area (or
diameter). Our calculation allows you to select a variety of units.
Thank you for your interest in the LMNO Engineering newsletter,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com.
(c) 2010 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, Ohio 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. December 1, 2009
Critical Depth in Circular Pipe
https://www.LMNOeng.com/Channels/CriticalDepth.php
For water flowing less than full in a pipe, it is important to know the critical depth. Though water may not actually be flowing at the critical depth, it is helpful to know if the actual water depth is greater than or less than critical. Critical depth is a quantity of fundamental importance to understanding flow characteristics in an open channel.
If the actual depth is greater than critical depth, then the flow is considered "subcritical". Subcritical flow is "slow flow" and is impacted by downstream conditions and will have a different flow profile than "supercritical flow".
If the actual depth is less than critical depth, then the flow is supercritical. Supercritical flow is "fast flow" and is impacted by upstream conditions. The water flows faster than its wave speed and is unimpacted by downstream conditions.
As water flows down a partially full pipe, the depth may change and pass through the critical depth if the bottom slope, geometry, or pipe material changes. If the flow is initially subcritical and the channel slope increases, the water may undergo a hydraulic drop if flow transitions from subcritical to supercritical. Conversely, if the flow is supercritical and the culvert slope becomes flatter, then there could be a hydraulic jump such that the water passes through the critical depth as it becomes subcritical.
The critical depth is computed from mass and energy principles. Equations are shown at https://www.LMNOeng.com/Channels/CriticalDepth.php.
Thank you for your interest in the LMNO Engineering newsletter,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
You received this free newsletter because you requested it at our website. If you no longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com.
(c) 2009 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, Ohio 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. November 3, 2009
Instantaneous Valve Closure - Compare two programs
Maximum pressure using Joukowski equation: https://www.LMNOeng.com/WaterHammer/impulse.php
Maximum pressure using general program based on numerical methods: https://www.LMNOeng.com/WaterHammer/WaterHammer.php
In my last newsletter, I showed that our impulse.php calculation is used to compute the maximum pressure surge due to an instantaneous valve closure. It also computes how fast the valve must be closed to be considered an instant valve closure.
Now I will show how our general water hammer calculation, which allows the user to enter the valve closure or opening time, gives the same result as the rapid closure calculation.
Example: Water flows steadily out of a reservoir through an 8-inch Schedule 40 horizontal steel pipe (inside diameter 7.981 inch, wall thickness 0.322 inch). The water level in the reservoir is 10 ft above the centerline of the pipe. The flow is regulated to a steady flow of 0.05 cfs by adjusting a valve 100 ft downstream of the reservoir. The valve suddenly closes. What is the expected maximum pressure increase and maximum measured pressure in the pipeline?
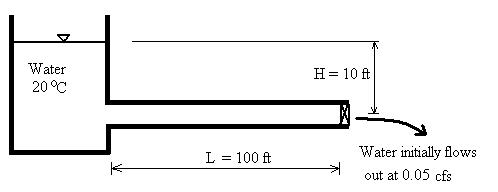
Unit conversions: Pipe inside diameter = D = 7.981 inch = 0.6651 ft = 20.27 cm. Flowrate = Q = 0.05 cfs = 22.44 gpm (US gallons) = 0.001416 m3/s. Reservoir water surface = H = 10 ft = 3.048 m.
Our impulse.php calculation requires entering the steady state velocity (V). V=Q/A,
where:
A = Pipe inside cross-sectional area = π D2 /4 = π (0.6651 ft)2
/4=0.3474 ft2.
V = Q/A = (0.05 ft3/s)/(0.3474 ft2) = 0.1439 ft/s.
The screen capture below from https://www.LMNOeng.com/WaterHammer/impulse.php shows that the maximum pressure surge is 19.4 ft of water (i.e. 8.38 psi). The valve is closed instantly if it is closed in less than 0.0462 seconds.
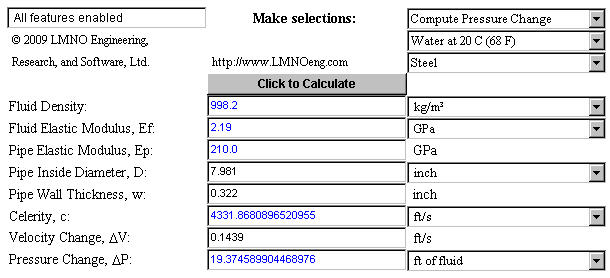

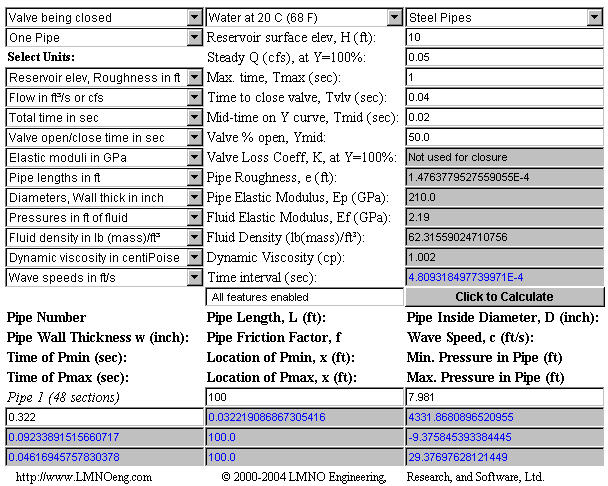
For our WaterHammer.php calculation, entering a reservoir surface elevation of 10 ft,
flowrate of 0.05 cfs, maximum time for the calculation somewhat larger than the valve
closure time, a valve closure time equal to or less than 0.0462 seconds, pipe wall
thickness, length, and inside diameter, a maximum pressure of 29.4 ft of water (i.e. 12.7
psi) is predicted. This is the maximum pressure that a pressure gage would read if located
just upstream of the valve. The program indicates that the maximum pressure occurs at
0.0462 seconds (in agreement with impulse.php), the time required for a pressure wave to
bounce off the closed valve, go upstream to the reservoir, and then return to the valve (a
time of 2L/c). If the reservoir elevation is subtracted from the pressure, we can compute
the pressure rise:
Pressure Rise = 29.4 ft - 10 ft = 19.4 ft of water (i.e. 8.38 psi). This is the same
pressure as computed by the impulse.php calculation. Pressures are gage pressures (i.e.
relative to atmospheric pressure).
https://www.LMNOeng.com/WaterHammer/WaterHammer.php:
If you have any questions about this newsletter, please let me know. Thank you,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com.
(c) 2009 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, Ohio 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. October 6, 2009
Instantaneous Valve Closure - Water Hammer
https://www.LMNOeng.com/WaterHammer/impulse.php
When a valve is closed rapidly, a pressure surge results. How significant is the surge?
Our newest calculation predicts the pressure increase due to a rapid valve closure. All
equations are shown on the web page.
Let's look at an example:
Water flows steadily out of a reservoir through an 8-inch Schedule 40 horizontal steel
pipe (inside diameter 7.981 inch, wall thickness 0.322 inch) at 4 ft/s. The pipe is 100 ft
long and has a valve at the end. The valve suddenly closes. How much will the pipeline
pressure increase due to the valve closure?
Answer: The rise in pressure is predicted to be 233 psi due to the instantaneous valve
closure.
Note: 7.981 inch= 20.27 cm, 0.322 inch= 0.818 cm, 4 ft/s= 1.22 m/s, 233 psi= 16.1 bar)
How fast is an instantaneous valve closure? To be considered an instantaneous closure, the
valve would need to close faster than the time required for a pressure wave to travel two
pipeline lengths. When a valve closes at the downstream end of a pipeline, a pressure wave
propagates upstream, bounces off the upstream reservoir/pipe connection, and propagates
back down to the valve. Thus, the pressure wave travels two pipeline lengths to get back
down to the closed valve. The valve must close quicker than this time period to be
considered instantly closed.
In our example, the wave speed (celerity) is 4332 ft/s. Thus:
Instant valve closure if closure time < 2L/c with L=pipe length, c=celerity
Therefore: 2L/c=2(100 ft)/(4332 ft/s)=0.046 seconds
In this example, a closure time less than 0.046 seconds is considered instantaneous. If
the valve takes longer than 0.046 seconds to close, the pressure rise would be less than
233 psi.
The type of liquid, velocity, pipe material, pipe diameter, and pipe wall thickness affect
the magnitude of the pressure surge. Additionally, the pipe length affects the definition
of instantaneous valve closure time.
My next newsletter will compare our instantaneous valve closure calculation with our other
water hammer calculation which allows you to enter a valve closure time.
Thank you for your interest in the LMNO Engineering newsletter,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com.
(c) 2009 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, Ohio 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. August 27, 2009
Hydraulic Jump
A hydraulic jump occurs in an open channel when the upstream flow is supercritical (Froude
Number>1) and there is a flow impediment downstream. The downstream impediment could be
a weir, a bridge abutment, a dam, a change in slope, a change in geometry, or simply
channel friction. The water depth increases during a hydraulic jump and energy is
dissipated as turbulence. Often, engineers will purposely install impediments in channels
in order to force jumps to occur. Mixing of coagulant chemicals in water treatment plants
is often aided by hydraulic jumps.
A photograph of a hydraulic jump is shown at https://www.LMNOeng.com/Channels/HydraulicJump.php
(flow from left to right) and a video is shown at http://www.youtube.com/watch?v=7QXrGN3tWP0
(flow from right to left).
The downstream water depth and energy loss across a hydraulic jump are computed from the
continuity (i.e. mass), momentum, and energy conservation equations. The velocity across a
jump decreases as the depth increases.
For a horizontal rectangular channel with (ft=foot, gpm=US gallons per minute, cfs=cubic
ft per second):
B = Width = 6 inch = 0.5 ft
Q = Discharge = 100 gpm = 0.2228 cfs (ft3/s)
Y1 = Upstream water depth = 1.0 inch = 0.08333 ft
Then (equations from https://www.LMNOeng.com/Channels/HydraulicJump.php):
V1 = Upstream velocity = Q/(B Y1) = (0.2228 cfs) / [(0.5 ft)(0.08333
ft)]
= 5.347 ft/s
F1 = Upstream Froude Number = V1/(g Y1)2
= (5.347 ft/s) / [(32.174 ft/s2)(0.08333 ft)]0.5 = 3.265
(g=acceleration of gravity)
Y2 = Downstream water depth = 0.5 Y1 [(1 + 8 F12)0.5
- 1]
= (0.5)(0.08333 ft) {[1 + 8 (3.266)2 ]0.5 - 1} = 0.3454 ft = 4.144
inch
V2 = Downstream velocity = Q/(B Y2) = (0.2228 cfs) / [(0.5
ft)(0.3455 ft)]
= 1.290 ft/s
F2 = Downstream Froude Number = V2/(g Y2)0.5
= (1.290 ft/s) / [(32.174 ft/s2)(0.3455 ft)]0.5 = 0.3869
h = Energy (i.e. head) loss across jump = (Y2-Y1)3 / (4 Y1
Y2)
= (0.3455 ft - 0.08333 ft)3 / [(4)(0.08333 ft)(0.3455 ft)] = 0.1565 ft = 1.878
inch
The above equation for h is useful since it only is a function of depths. However, the
equation is identical (Chaudhry, 1993, p. 181) to the common form of the energy equation
in a horizontal rectangular channel:
h = (V12 - V22)/(2g) + Y1 - Y2
= [(5.347 ft/s)2 - (1.290 ft/s)2] / [(2)(32.174 ft/s2)] +
0.08333 ft - 0.3455 ft
= 0.1563 ft = 1.876 ft
(difference with this h and previous h due to rounding intermediate computations)
The length of the jump in a horizontal rectangular channel can be computed from
(https://www.LMNOeng.com/Channels/HydraulicJump.php):
L = Jump length = 220 Y1 tanh[(F1 - 1) / 22]
= 220 (0.08333 ft) tanh[(3.266-1)/22] = (220)(0.08333 ft) tanh(0.1030)
tanh() is hyperbolic tangent. Some calculators have this function, some do not. A
definition it terms of ez (exponential function) can be found at http://mathworld.wolfram.com/HyperbolicTangent.html.
tanh(0.1030) = 0.1026 Therefore:
L = (220)(0.08333 ft)(0.1026) = 1.881 ft
Thus, water at a 1-inch depth flowing at 100 gpm in a 6-inch wide horizontal rectangular
channel has upstream and downstream velocities of 5.35 ft/s and 1.29 ft/s; and upstream
and downstream Froude Numbers of 3.27 and 0.387, all respectively. The downstream depth,
head loss, and jump length are computed as 4.15 inch, 1.88 inch, and 1.88 ft,
respectively.
If you have any questions about this newsletter or have ideas for future newsletters, I
would like to hear from you. Best regards,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
Reference:
Chaudhry, M. Hanif. 1993. Open-Channel Flow. Prentice-Hall.
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com.
(c) 2009 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, Ohio 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. May 29, 2008
Videos of Experiment and Analysis of Water Discharging from a Tank
https://www.LMNOeng.com/Video
We have recently made some movies of a fluid mechanics experiment and its analysis. One of
the videos shows water discharging steadily from a tank through a 0.25 inch diameter
orifice. The head, flowrate, horizontal trajectory, and vertical trajectory are measured.
The other two videos show how equations and the calculation at our Tank Discharge page can
be used to predict the experimental results.
The basic equation for steady discharge from an orifice in terms of head is
( from https://www.LMNOeng.com/TankDischarge.php
):
Q = Co A (2gh)0.5
where
A = area of orifice (ft2)
Co = orifice coefficient = 0.61 for a sharp-edged orifice
g = acceleration of gravity = 32.174 ft/s2
h = head (ft)
Q = flowrate (i.e. discharge) out of the orifice (ft3/s)
Alternatively, to compute discharge from the trajectory:
Q = Cc A X [g/(2Y)]0.5
where
Cc = contraction coefficient of orifice = 0.62 for a sharp-edged orifice
X = horizontal trajectory (ft)
Y = vertical trajectory (ft)
Any other consistent set of units can be used in the equations.
Also, note that Co = Cc Cv
where Cv = velocity coefficient = 0.98 for a sharp-edged orifice
Please let me know if you have any questions or are interested in other experiments.
Thank you for your interest in the LMNO Engineering newsletter,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com.
(c) 2008 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, Ohio 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. February 14, 2008
Fire Hydrant Pressure Requirement
Fire hydrants may appear to be mundane pieces of equipment, having been around - in one
form or another - for centuries. These fairly simple pieces of equipment can require
higher main line pressures than expected in order to obtain the expected flow.
For instance, consider the case of a hydrant located on a 6-inch diameter pipe. A flow
test is conducted where the 2.5-inch diameter nozzle is open and allowed to flow freely to
the atmosphere.
The energy equation for an incompressible liquid is written from the 6-inch diameter pipe
at the hydrant inlet to the 2.5-inch nozzle discharging to atmospheric pressure:
Zp + Pp/S + Vp2 /(2g) = Zn + Pn/S
+ Vn2 /(2g) + Loss/S
where (ft=feet, s=second, psi=pounds per square inch gage, psf=pounds per square ft gage,
cfs = ft3/s; gage means relative to atmospheric pressure):
g = Acceleration due to gravity = 32.2 ft/s2
Loss = Friction and other losses within the hydrant, psf
Pn = Pressure at 2.5-inch nozzle discharging to the atmosphere = 0 psf
Pp = Pressure in 6-inch diameter pipe at inlet to fire hydrant, psf
S = Specific weight of water (not specific gravity) = 62.4 lb/ft3
Vn = Velocity in 2.5-inch nozzle as it discharges to the atmosphere, ft/s
Vp = Velocity in 6-inch pipe, ft/s
Zn = Elevation of 2.5-inch nozzle, ft
Zp= Elevation of pipe, ft
A hydrant typically is supposed to have no more than about a 5 psi pressure loss. The
height of the 2.5-inch nozzle above the hydrant inlet is about 6 ft. Hydrants are often
desired to have a flow of 1000 gpm. Therefore, for this case:
Zn - Zp = 6 ft
Loss = (5 psi)(144 in2/ft2) = 720 psf
Q = Flow = (1000 gpm)(cfs/448.8 gpm) = 2.228 cfs
Dn = Diameter of nozzle = (2.5 in)(ft/12 in) = 0.2083 ft
An = Nozzle area = (pi/4)(0.2083 ft)2 = 0.03409 ft2
Ap = Area of 6-inch pipe = (pi/4)(0.5 ft)2 = 0.1963 ft2
Vn = Q/An = (2.228 cfs)/(0.03409 ft2) = 65.36 ft/s
Vp = Q/Ap = (2.228 cfs)/(0.1963 ft2) = 11.35 ft/s
Then,
Vn2/(2g) = (65.36 ft/s)2 / [(2)(32.2 ft/s2)] =
66.33 ft
Vp2/(2g) = (11.35 ft/s)2 / [(2)(32.2 ft/s2)] =
2.000 ft
Loss / S = (720 lb/ft2) / (62.4 lb/ft3) = 11.54 ft
Now, solve for Pp using the energy equation:
Pp/S = (Zn - Zp) + Pn/S + Vn2/(2g)
- Vp2(2g) + Loss/S
= 6 ft + 0 ft + 66.33 ft - 2.000 ft + 11.54 ft
= 81.87 ft
Then,
Pp = (81.87 ft)(62.4 lb/ft3)(ft2/144 in2) =
35.5 psi
Thus, a pressure of 35.5 psi is required to push 1000 gpm from a 6-inch pipe through the
hydrant internals, up 6 ft, and out the 2.5-inch nozzle to the atmosphere.
Alternatively, if the 4.5-inch nozzle was flowing to the atmosphere (instead of the
2.5-inch nozzle), then:
An=(pi/4)(4.5/12 ft)2 = 0.1104 ft2
Vn=(2.228 cfs)/(0.1104 ft2) = 20.17 ft/s
Vn2/(2g) = (20.17 ft/s)2 / [(2)(32.2 ft/s2)] =
6.319 ft
Then,
Pp/S = 6 ft + 0 ft + 6.319 ft - 2.000 ft + 11.54 ft
= 21.9 ft
and
Pp = (21.9 ft)(62.4 lb/ft3)(ft2/144 in2) = 9.5
psi
Thus, a pressure of only 9.5 psi is required to push 1000 gpm from a 6-inch pipe through
the hydrant internals, up 6 ft, and out the 4.5-inch nozzle to the atmosphere.
The difference in pressures (35.5 psi versus 9.5 psi) is attributable to the higher
velocity head that must be overcome for flow out of the smaller nozzle.
One could do the calculation in reverse to compute the flow out of the 2.5-inch or
4.5-inch nozzle for a given pressure in the 6-inch pipe. Often, water systems are designed
to deliver 20 psi at hydrant inlets.
The calculations assume an elevation change of 6 ft from the 6-inch pipe to the nozzle
discharge and a loss of 5 psi through the hydrant. Additional loss due to the water
contracting to a "vena-contracta" diameter of less than the nozzle diameter as
it flows out of a nozzle was not included.
I hope that this newsletter has demonstrated the significant impact of exit nozzle
velocity head on required pressure for flow out of a hydrant that is freely discharging to
the atmosphere, as in a hydrant flow test.
Thank you for your interest in the LMNO Engineering newsletter,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com.
(c) 2008 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, Ohio 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. November 13, 2007
Thank you for opting-in to our newsletter. It has been about a year since I sent a fluid
flow newsletter. If you no longer wish to be on our list, simply respond and put
"Discontinue newsletter" in the subject line. Though new people opt-in
regularly, some people have been on our newsletter list for 9 years and may no longer be
interested.
There are now over 60 fluid flow calculations on our website. To show our appreciation for
our newsletter subscribers, please use the following free PIN number: LMNOeng (use exact
capitalization). Enter the PIN at our home page https://www.LMNOeng.com . All of the
calculations will be enabled until November 21, 2007.
Here is a summary of the calculations we have on our site:
Closed conduit (pressurized flow) calculations for computing flowrate, pressure drop,
elevation change, pump head, or pipe diameter using the Darcy-Weisbach or Hazen-Williams
method for friction losses. Hazen-Williams is primarily used for municipal water supply
pipes while Darcy-Weisbach is valid for other liquids in addition to water.
Weymouth and Panhandle methods for compressible gas flow.
Pipe network calculation for up to 12 pipes and 9 nodes.
Orifice, nozzle, and venturi flowmeter calculations based on ISO and ASME standards.
Force due to a pipe bend. Discharge from a tank.
Open channel flow calculations for Manning's equation and inlet/outlet control.
Inverted siphon for piping storm water under a river.
Flumes, weirs. Hydraulic jump calculator.
Runoff and detention basin sizing. Groundwater and contaminant migration.
Volume calculators for inclined and horizontal cylinders (tanks).
Gas density, viscosity, unit conversions.
Please let me know if you have any questions. I plan to write newsletters every few months
with technical information about fluid flow. Please see my past newsletters that are
listed at the bottom of our home page.
Thank you for your interest in the LMNO Engineering newsletter,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com .
(c) 2007 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, OH 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. October 23, 2006
End Depth Method for Flow Measurement in Open Channels
Ever wish you could determine the discharge (Q) of water out of a culvert? Maybe you
thought about using Manning's equation - but you needed to measure the slope and estimate
the Manning coefficient (n). And you realized that a small error in estimating n can give
a large error in Q. Maybe you found Q by measuring the time to fill a 20 liter bucket. For
high flows, the time is too short to measure accurately; and larger buckets get too heavy.
The end depth method doesn't require a slope measurement or an estimation of n. It is
based solely on the water depth (h) and diameter (D) of the culvert. It requires that the
culvert be essentially horizontal and that the water drops off a height greater than h.
We have end depth calculations for circular culverts, rectangular channels, and triangular
channels that have sudden drop-offs (like a waterfall). The rectangular and triangular
channel calculations are fully functional without paying our registration fee. You can see
the rectangular channel calculation at https://www.LMNOeng.com/Waterfall/waterfall.php
.
Thank you for your interest in the LMNO Engineering newsletter,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
LMNO Engineering's previous newsletters can be viewed at https://www.LMNOeng.com/Newsletters/newsletter8.htm
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com .
(c) 2006 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, Ohio 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. August 21, 2006
Partially Full Inclined Cylinder Volume Calculation
https://www.LMNOeng.com/Volume/InclinedCyl.php
Last month we completed a calculation that many visitors have requested over the past few
years. It computes the volume of liquid contained in a partially full inclined cylinder.
It can be used for computing the oil volume in a storage tank that is not horizontal. Or
the volume of water in a pipeline that is sloped. The user enters the cylinder diameter,
length, and angle from horizontal.
The calculation allows you to enter the liquid depth measurement several ways:
1. Vertical distance from bottom of tank to liquid surface.
2. Vertical distance from top of tank down to liquid surface.
3. Distance from bottom of tank to liquid surface measured perpendicular to bottom of
tank.
4. Distance from top of tank to liquid surface measured perpendicular to top of tank.
Since the cylinder is at an angle, the user must also indicate how far from the downstream
edge of the tank the depth measurement is made.
A full description of the governing equations, inputs, and outputs are shown on the web
page https://www.LMNOeng.com/Volume/InclinedCyl.php.
If you are interested in the mass of liquid in the tank, just multiply the output volume
by the liquid density.
I hope you find the calculation helpful. Thank you for your interest in the LMNO
Engineering newsletter,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
LMNO Engineering, Research, and Software, Ltd.
https://www.LMNOeng.com
LMNO Engineering's previous newsletters can be viewed at https://www.LMNOeng.com/Newsletters/newsletter8.htm
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com .
(c) 2006 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, Ohio 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. May 16, 2006
Gas flow conversions
https://www.LMNOeng.com/Flow/GasFlow.php
We have completed a new calculation called Gas Flow Conversions. There is often confusion
about how gas flowrates are stated, so we developed the calculation to aid in unit
conversions for gas flow. Some gas flows are expressed in mass units, like kg/s or lb/day.
Sometimes, flow units are acfm, scfm, or Nm3/s, to name a few.
Mass flowrate is straightforward. It is the amount of mass flowing per unit time.
Volumetric flowrates, however, are either expressed as flow at "actual
conditions" or flow at "standard (or normal) conditions". Units for flow at
actual flowing conditions often have the letter "a" in front of the unit.
In contrast to flow at actual conditions, flows can be expressed at standard (or normal)
conditions. English units usually are prefaced with the word "standard" or
letter "s" while metric units are usually prefaced with the word
"normal" indicated by the letter "N" (don't confuse with the Newton
unit).
Standard (or normal) flows are the volume equivalent to actual flow if the actual flow
were at standard temperature and pressure. For the same mass and temperature of gas, one
cubic meter of a gas at 10 atmospheres of pressure occupies much more volume when its
pressure is reduced to 1 atmosphere. Think of gas in a cylinder acted on by a piston.
Please see our web page https://www.LMNOeng.com/Flow/GasFlow.php
for equations and further discussion of gas conversions.
Thank you for your interest in the LMNO Engineering newsletter,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
LMNO Engineering, Research, and Software, Ltd.
https://www.LMNOeng.com
LMNO Engineering's previous newsletters can be viewed at https://www.LMNOeng.com/Newsletters/newsletter8.htm
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com.
(c) 2006 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, Ohio 45701 USA (740) 707-2614
LMNO@LMNOeng.com
Newsletter. April 4, 2006
Culvert Design using Inlet and Outlet Control
https://www.LMNOeng.com/Pipes/hds.php
Culverts have been utilized for thousands of years as a means to transmit water under
walkways and roads. Too often, culverts are selected without sufficient thought of how
much water needs to be conveyed under extreme conditions. If a culvert cannot convey all
of the incoming water, then the water will flow over or around the pipe - or simply back
up behind the culvert creating a pond or reservoir. If any of these conditions are
unacceptable, then the proper culvert diameter and number of culverts must be selected
prior to installation in order to convey all of the anticipated water through the pipe(s).
Discharge through a culvert is controlled by either inlet or outlet conditions. Inlet
control means that flow through the culvert is limited by culvert entrance
characteristics. Outlet control means that flow through the culvert is limited by friction
between the flowing water and the culvert barrel. The term "outlet control" is a
bit of a misnomer because friction along the entire length of the culvert is as important
as the actual outlet condition (the tailwater depth). Inlet control most often occurs for
short, smooth, or greatly downward sloping culverts. Outlet control governs for long,
rough, or slightly sloping culverts. The type of control also depends on the flowrate. For
a given culvert installation, inlet control may govern for a certain range of flows while
outlet control may govern for other flowrates. If the flowrate is large enough, water
could go over the road (or dam). In this case, our calculation automatically computes the
amount of water going over the road and through each culvert, as well as the headwater
depth.
Our culvert design calculation aids the designer in selecting the number of culverts and
culvert diameter. It also plots headwater depth vs. discharge so that the designer can
view culvert performance over a wide range of flows. Our calculation is primarily based on
the methodology presented in Hydraulic Design of Highway Culverts by Normann (1985) and
published by the USA Department of Transportation's Federal Highway Administration.
Please see https://www.LMNOeng.com/Pipes/hds.php
to run the calculation and to see equations, diagrams, and additional description.
Thank you for your interest in the LMNO Engineering newsletter,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
LMNO Engineering, Research, and Software, Ltd.
https://www.LMNOeng.com
Reference:
Normann, J. M. 1985. Hydraulic design of highway culverts. HDS-5 (Hydraulic Design Series
5). FHWA-IP-85-15. (2005 update viewable at http://isddc.dot.gov/OLPFiles/FHWA/012545.pdf
- file size is 9MB)
LMNO Engineering's previous newsletters can be viewed at https://www.LMNOeng.com/Newsletters/newsletter8.htm
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com .
(c) 2006 LMNO Engineering, Research, and Software, Ltd.
LMNO Engineering, Research, and Software, Ltd.
The fluid flow calculations website: https://www.LMNOeng.com
7860 Angel Ridge Rd. Athens, Ohio 45701 USA +1(740) 707-2614
LMNO@LMNOeng.com
Newsletter. February 9, 2006.
Newsletter Topics
Many of you have been newsletter subscribers for a long - possibly since 1998 when we
started LMNO Engineering. Others are more recent newsletter subscribers. If there are any
topics you would like to learn about, please let me know by emailing me at LMNO@LMNOeng.com .
Over the years, I have written newsletters regarding many aspects of fluid flow, which
relate to our software. These topics have included pressurized pipe flow and flow
measurement; flow of gases and liquids in pipes; networks of parallel and series pipes;
orifice, nozzle, venturi flow meters; and the Bernoulli equation. I have written about
open channel flow in circular pipes and trapezoidal channels; gradually varied flow
profiles; inverted siphons for carrying stormwater or wastewater under roads or rivers;
culvert design using inlet and outlet control; and weirs and flumes for flow measurement.
There have been newsletters about watershed runoff - time of concentration, Rational
equation, TR-55 method. And groundwater flow and contaminant transport.
All of the past newsletters are listed at the bottom of our home page
https://www.LMNOeng.com . Thank you for your interest in the LMNO Engineering newsletter,
Ken Edwards, Ph.D., P.E. (Owner/Engineer/Programmer)
LMNO Engineering, Research, and Software, Ltd.
https://www.LMNOeng.com
LMNO Engineering's previous newsletters can be viewed at https://www.LMNOeng.com/Newsletters/newsletter8.htm
You received this free newsletter because you requested it at our website. If you no
longer wish to receive it, send a message stating "Discontinue Newsletter" to LMNO@LMNOeng.com.
(c) 2006 LMNO Engineering, Research, and Software, Ltd.
© 2006-2025 LMNO Engineering, Research, and Software, Ltd. All rights reserved.
LMNO Engineering, Research, and Software, Ltd.
7860 Angel Ridge Rd. Athens, Ohio 45701 USA Phone: (740) 707‑2614
LMNO@LMNOeng.com
https://www.LMNOeng.com
