Units: C=degrees Celsius, cm=centimeter, cP=centipoise, cSt=centistoke, F=degrees Fahrenheit, cfm=cubic feet per minute, cfs=cubic feet per second, ft=foot, g=gram, hr=hour, in=inch, K=degrees Kelvin, kg=kilogram, lb=pound, m=meters, mbar=millibar, min=minute, mm=millimeter, N=Newton, Pa=Pascal, psi=pound per square inch, R=degrees Rankine, s=second, scfm=standard cfm, std=standard.
Pressure Taps for Large Bore Orifice Meter
Introduction
Orifice flow meters are used to determine a liquid or gas flow rate by measuring the
differential pressure (P1 - P2) across the orifice plate.
Orifice flow rate measurement meters are typically less expensive to install and manufacture than the other
commonly used differential pressure flow rate meters; however, nozzle
and venturi flow rate meters have the advantage of lower pressure
drops. Equations for orifice flow rate measurement meters have the advantage of no Reynolds Number upper
limit for validity.
An orifice flow rate measurement meter is typically installed between flanges connecting two pipe sections (flanges are not shown in the above drawings). The three standard pressure tapping arrangements are shown in the drawings; the location of the pressure taps affects the discharge coefficient somewhat. Flange pressure taps penetrate the flange and are at a standard distance of 1 inch (2.54 cm) from either side of the orifice. For corner taps or D and D/2 taps, the pressure tap locations are as shown.
Orifices are typically less than 0.05D thick. For exact geometry and specifications for orifices, see ISO (1991) or ASME (1971). The ASME and ISO have been working on guidelines for orifices for flow rate measurement since the early 1900s. The organizations have the most confidence in orifice accuracy when the Reynolds number exceeds 105, though Reynolds numbers as low as 4x103 are valid for certain d/D ratios as discussed below. The flow rate measurement calculation above is for flow rate measurement of gases. For liquid flow through orifices, please visit our orifice flow rate measurement calculations for liquids: Pipe diameter < 5 cm or pipe diameter ≥ 5 cm. Gas flow rate measurement calculations include an expansibility factor (e), which is not present in the liquid flow rate measurement calculation. The expansibility factor accounts for the effect of pressure change on gas density as gas flows through the orifice. LMNO Engineering also has an orifice calculation for gas flow rate measurement in pipes less than 5 cm diameter.
Equations
The flow rate measurement calculations on this page are for orifices carrying a gas as described in ISO (1991 and 1998).
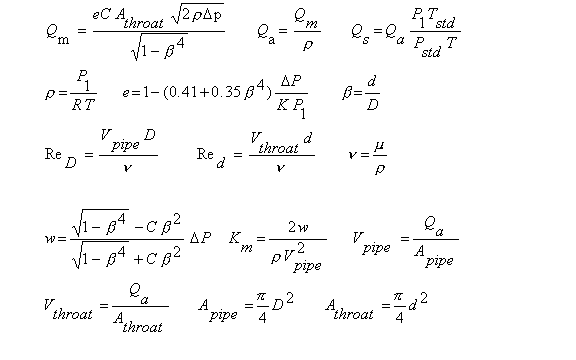
Discharge Coefficient (ISO, 1998)
Corner Pressure Taps: L1 = L'2 = 0
D and D/2 Pressure Taps: L1 = 1 and L'2 = 0.47
Flange Pressure Taps: L1 = L'2 = 0.0254/D where D is in
meters
Validity and Discussion
Discharge Coefficient for Gas Flow Rate Measurement:
For all types of pressure taps: d ≥ 1.25 cm, 5 cm ≤ D ≤ 1
m, 0.1 ≤ d/D ≤ 0.75
For Corner Pressure Taps or D and D/2 Pressure Taps:
ReD ≥ 4000 for 0.1 ≤ d/D ≤
0.5 and ReD ≥ 16,000(d/D )2 for
d/D>0.5
For Flange Pressure Taps: ReD ≥ 4000 and ReD ≥ 170,000 D (d/D )2 where D is in meters
The calculation does not provide results if these values are out of range.
Expansibility:
The equation shown above for expansibility, e, is valid for P2/P1
≥ 0.75. Our flow rate measurement calculation gives a warning message if P2/P1
< 0.75, but still computes answers.
Built-in Properties for Certain Gases in Flow Rate Measurement Calculation:
To provide ease of use, our flow rate measurement calculation has properties of some gases built-in to the
calculation. The user can select Air, Carbon dioxide, Hydrogen, Methane (natural
gas), Nitrogen, or Oxygen. The density is automatically computed using the ideal gas
law based on the upstream pressure and temperature entered into the gas flow rate measurement calculation. The dynamic viscosity is
a function of temperature and uses the methodology shown on our Gas
Viscosity page. The isentropic exponent, K, is based on the specific
heat ratio. For methane, the dynamic viscosity value shown in the flow rate measurement calculation is
valid for 0 oF < T < 1000 oF. If T<0
oF, then the viscosity value shown and used in the flow rate measurement computation is the viscosity at 0
oF. If T>1000 oF, then the viscosity value shown and used
in the flow rate measurement computation is the viscosity at 1000 oF (0 oF is -17.8 oC
and 1000 oF is 537.8 oC). For all other gases shown in the
drop-down menu, there is no temperature limitation on the validity of the viscosity.
Dynamic viscosity is essentially independent of pressure.
If you know that your density, viscosity, or isentropic exponent is significantly different than the value shown in the flow rate measurement calculation, then you can select "User enters P1, density, viscosity, K" and enter these values manually. Also, if the gas is not listed in our drop-down menu, then you can select "User enters P1, density, viscosity, K" and enter these values manually. K must be > 1. Additionally, values for K can be found in Weast (1985, p. F-11), Perry and Green (1984, p. 3-144), and other sources.
Note that our flow rate measurement calculation prior to February 2003 included helium as a gas in the drop-down gas menu, and the viscosities for the gases were set at 20 oC. Now, the viscosity variation with temperature is included, but helium was removed because it doesn't have a simple viscosity relationship with temperature.
ISO Pipe Roughness Recommendation:
ISO recommends that in general k/D ≤ 3.8x10-4 for
Corner Taps and k/D ≤ 10-3 for Flange or D and D/2
pressure taps. k is the pipe roughness.
Our flow rate measurement calculation does not check this.
Pressure Loss:
w is the static pressure loss occurring from a distance of approximately D
upstream of the orifice to a distance of approximately 6D downstream of the
orifice. It is not the same as differential pressure. Differential pressure is
measured at the exact locations specified in ISO (1991) (shown in the above figures).
Minor Loss Coefficient:
Km is computed to allow you to design pipe systems with orifices and
incorporate their head loss. Head loss is computed as h=KmV2pipe/2g.
Standard Volumetric Flow Rate:
Standard volumetric flow rate, Qs, is the volumetric flow rate
computed at standard pressure and temperature, Pstd and Tstd
(shown below in Variables). Actual flow rate, Qa,
is computed at the gas's actual pressure and temperature. Qs is
useful to users who need to compute (or input) standard flow rate; often pump curves and
flow measurement devices provide standard, rather than actual, flow rate. The
advantage of using standard flow instead of actual flow is that the same device (or pump
curve) can be used for a gas at various temperatures and pressures without re-calibrating
for an infinite range of actual pressures and temperatures. The user can easily
convert standard to actual flow rate if the actual temperature and pressure of the gas are
known; our flow rate measurement calculation does this automatically.
Variable Definitions
Dimensions: F=Force, L=Length, M=Mass, T=Time, t=temperature. Note F=M-L/T2.
Bore diameter and throat diameter both refer to d.
A = Area [L2], C = Discharge Coefficient, d = Throat Diameter [L], D = Pipe Diameter [L], e = Gas Expansibility, h = Head Loss [L], k = Equivalent Roughness of Pipe Material [L], K = Gas Isentropic Coefficient, Km = Minor Loss Coefficient, M = Mass Flow Rate [M/T], P1 = Upstream Absolute Pressure [F/L2], P2 = Downstream Absolute Pressure [F/L2], Δp = Differential Pressure [F/L2] = P1-P2, Pstd = Standard Atmospheric Pressure = 14.73 psia = 1.016x105 N/m2, Qa = Actual Volumetric Flow Rate [L3/T], Qs = Volumetric Flow Rate at Standard Pressure and Temperature [L3/T], R = Gas Constant (used to compute gas density) = 8312/W N-m/kg-K, Red = Reynolds Number based on d, ReD = Reynolds Number based on D, T = Gas Temperature [t] (converted automatically to absolute), Tstd = Standard Absolute Temperature = 520oR = 288.9K, V = Velocity [L/T], w = Static Pressure Loss [F/L2], W = Molecular Weight of Gas [gram/mole], β = Ratio d/D, ρ = Gas Density [M/L3], μ = Gas Dynamic Viscosity [F-T/L2]. ν = Gas Kinematic Viscosity [L2/T].
Error Messages
"P2/P1<0.75. Out of range". The
equation for expansibility, e, is only valid for P2/P1≥0.75.
This is a just a warning message; all variables are computed.
For the following error messages, only some variables are computed by the flow rate measurement calculation. For example if
throat diameter (d) is to be computed, then pressure ratio, expansibility, pipe area, pipe
velocity, ReD, and some other variables will be computed and shown.
However, if ReD is out of range for C to be valid, then C and d (and anything
depending on d - such as throat area and throat velocity) will not be computed. If
an error message is shown and you think your input is correct, be sure to check that you
have selected the correct units for your entries.
"Infeasible input". While none of the inputs alone are out of
range, they collectively result in a physically infeasible situation.
"P1 and T (abs) must be >0". Absolute pressure or
absolute temperature was entered as zero or negative. If temperature was entered in
C or F, it was internally converted to absolute temperature.
"P1,D, T(abs), Dens, Visc must be >0". Pipe diameter,
density, viscosity, absolute pressure, and/or absolute temperature was entered as zero or
negative.
"K must be >1". Isentropic exponent was entered as ≤ 1.
"d/D must be <1". Orifice diameter cannot exceed pipe
diameter in the flow rate measurement calculation.
"M or Q, and d must be >0". Mass flow rate, volumetric flow
rates, and/or orifice diameter were entered into the flow rate measurement calculation as zero or negative.
"d, D, d/D, or ReD out of range". At least one of
these variables is out of the range of validity for the discharge
coefficient.
"Δp and d must be >0". Cannot enter pressure difference or
d ≤0.
"Δp must be < P1". Differential pressure cannot
exceed P1; this would cause P2(absolute) to be <0 which is
impossible.
"d/D out of range", "D out of range", "d
out of range" These must be in the range of validity
shown above.
"M or Q, and Δp must be >0". Mass flow rate, volumetric
flow rates, and/or differential pressure were entered as zero or negative in the flow rate measurement calculation.
"ReD out of range". ReD must be in range of validity shown above.
"ReD will be too small", "ReD will be
out of range", "d/D will be out of range", "d will
be <0.0125 m", "d/D will be < 0.1", "d/D will
be > 0.75". Input values result in variables that will be out of the range of validity.
• Try the simpler orifice flow rate calculation on our Bernoulli page if your parameters are out of range. It is
not as accurate, but won't give "parameter out of range" error messages.
References
American Society of Mechanical Engineers (ASME). 1971. Fluid meters: Their
theory and application. Edited by H. S. Bean. 6ed. Report of ASME
Research Committee on Fluid Meters.
International Organization of Standards (ISO 5167-1). 1991. Measurement of fluid flow by means of pressure differential devices, Part 1: Orifice plates, nozzles, and venturi tubes inserted in circular cross-section conduits running full. Reference number: ISO 5167-1:1991(E).
International Organization of Standards (ISO 5167-1) Amendment 1. 1998. Measurement of fluid flow by means of pressure differential devices, Part 1: Orifice plates, nozzles, and venturi tubes inserted in circular cross-section conduits running full. Reference number: ISO 5167-1:1991/Amd.1:1998(E).
Perry, R. H. and D. W. Green (editors). 1984. Perry's Chemical Engineers' Handbook. McGraw-Hill Book Co. 6th ed.
Weast, R. C. (editor). 1985. CRC Handbook of Chemistry and Physics. Chemical Rubber Company. 65th ed.
© 2000-2025 LMNO Engineering, Research, and Software, Ltd. All rights reserved.
LMNO Engineering, Research, and Software, Ltd.
7860 Angel Ridge Rd. Athens, Ohio 45701 USA Phone: (740) 707‑2614
LMNO@LMNOeng.com
https://www.LMNOeng.com
