Surge Pressure Calculator
Pressure Wave Travel Time Calculator (free)
Copy and paste the celerity from the above water hammer calculation into the
calculation below to compute wave travel time (may need to use keyboard control‑c and control‑v
instead of right-clicking):
Units: cm=centimeter, ft=foot, g=gram, G=Giga, k=kilo, kg=kilogram, lb=pound, m=meter, M=Mega, mm=millimeter, N=Newton, Pa=Pascal, psf=pound per square foot, psi=pound per square inch, s=second.
Introduction
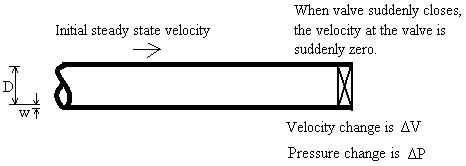
Prior to water hammer, liquid initially flows at a constant velocity through a pipe. A downstream valve closes instantaneously, and the liquid slams against the closed valve causing a pressure spike ΔP also called water hammer.
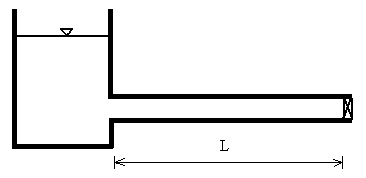
The pipe length L is defined as shown below for the case where there is a reservoir on the left:
Equations
The water hammer instantaneous valve closure calculation predicts the maximum increase in pressure that
will occur due to a sudden valve closure. The valve closure time in water hammer is considered to be
instantaneous if the valve closes faster than (or equal to) the time required for a
pressure wave to travel two pipe lengths (i.e. the time for the wave to travel upstream
from the valve, reflect off the upstream boundary and return to the valve).
The pressure
predicted by the water hammer instantaneous valve closure calculation provides the
engineer with the expected maximum pressure increase. The water hammer calculation can also be used in
reverse - to compute the pipe velocity - if a maximum pressure rise due to water hammer is input. For the
"Click to Calculate" button to function, the water hammer pressure calculation requires
registration, but the wave travel time calculation does not.
Joukowski Equation
One-dimensional momentum conservation for frictionless flow is used to derive the
Joukowski equation for water hammer. The equation was developed for a liquid flowing steadily through a
pipe and then instantly the velocity drops to zero due to a sudden valve closure in a water hammer event. The
water hammer equation assumes that liquid compression and pipe friction are negligible.
Though the
Joukowski equation's primary applicability is for a liquid velocity that drops to zero
upon contacting a closed valve causing water hammer, the equation is valid for any instantaneous drop in
velocity, not necessarily a drop to zero velocity. The Joukowski equation is seen with and
without a negative sign on the right hand side depending on whether the pressure wave is
traveling upstream or downstream in the water hammer event. In either case, the pressure increase due to water hammer is a positive
number. The Joukowski equation is (Wylie, 1993, p. 4; Chaudhry, 1987, p. 8; Hwang and Houghtalen, 1996, p. 118):
ΔP = ρ c ΔV
The equation for wave speed, c, during water hammer is based on mass conservation and allows the pipe wall material to expand (Wylie, 1993, p. 6; Chaudhry, 1987, p. 34; Hwang and Houghtalen, 1996, p. 115):
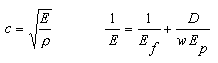
The ΔP equation for water hammer was derived for liquid upstream of the valve and does not include effects downstream of the valve. The D/(wEp) portion was derived using a thin-walled pipe approximation.
Water hammer Wave Travel Time Equation
Instantaneous valve closure due to water hammer is defined to occur if the valve is closed faster than the wave travel time. The wave travel time is (Hwang and Houghtalen, 1996, p. 119):
tw = 2L/c
In water hammer, the wave travel time, tw, is the time for a pressure wave to propagate from the valve, upstream to the reservoir, and back down to the valve. If a valve takes longer than tw to close, then our other water hammer calculation should be used, where the user can enter the valve closure time.
Variables
Dimensions: F=Force, L=Length, M=Mass, T=Time
c = Celerity (wave speed) [L/T].
D = Inside diameter of pipe [L].
E = Composite elastic modulus [F/L2].
Ef = Elastic modulus of fluid [F/L2].
Ep = Elastic modulus of pipe material [F/L2].
L = Pipe length [L].
tw = Wave travel time [T].
w = Pipe wall thickness [L].
ΔP = Maximum pipe pressure increase in water hammer event due to sudden valve closure [F/L2].
ΔV = Change in velocity in water hammer [L/T].
ρ = Fluid density [M/L3].
Fluid Properties, Pipe Properties, and Pipe Wall Thickness
Fluid Properties
Fluid density, viscosity, and elastic modulus provided by the drop-down menus in the water hammer calculation have been compiled from the closed conduit pipe flow references shown on our literature web page.
Pipe Properties
The pipe material elastic moduli built into our water hammer calculation have been compiled from the references shown below.
Error Messages
Pressure calculation
"Need Density > 0". "Need Ef > 0". "Need Ep > 0". "Need Diameter > 0". "Need Thickness > 0". Density, elastic modulus of fluid and pipe, diameter, and wall thickness must be entered as positive numbers in water hammer calculation.
"Need ΔV > 0". "Need ΔP > 0". If ΔV or ΔP is selected as an input, it must be positive in water hammer calculator.
Wave travel time calculation
"Need Length>0". "Need Celerity>0". Length and celerity (wave speed) must be entered as positive numbers.
References
Chaudhry, M. Hanif. 1987. Applied Hydraulic Transients. Van Nostrand Reinhold Co. 2ed.
Hwang, Ned H .C. and Robert J. Houghtalen. 1996. Fundamentals of Hydraulic Engineering Systems. Prentice Hall, Inc. 3ed.
LMNO Engineering, Research, and Software. 2009. Newsletter comparing water hammer calculations.
Mays, Larry W. 1999. Hydraulic Design Handbook. McGraw-Hill.
Wylie, E. Benjamin and Victor L. Streeter. 1993. Fluid Transients in Systems. Prentice-Hall, Inc.
© 2009-2026 LMNO Engineering, Research, and Software, Ltd. All rights reserved.
LMNO Engineering, Research, and Software, Ltd.
7860 Angel Ridge Rd. Athens, Ohio 45701 USA Phone: (740) 707‑2614
LMNO@LMNOeng.com
https://www.LMNOeng.com
