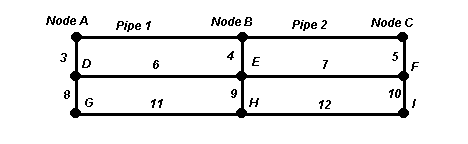
Enter positive values for inflows at nodes (negative values for outflows). Enter pipe diameter of 0.0 to make a pipe non-existent.
Register to enable "Calculate" button.
Units: bbls/day=barrels/day, cfm=ft3/min, cfs=ft3/s, cm=centimeter, cP=centipoise, cSt=centistoke, in=inch, in H2O=inch water at 60F, in Hg=inch mercury at 60F, ft=foot, g=gram, gpd=gallon (US)/day, gph=gallon (US)/hr, gpm=gallon ;(US)/min, hr=hour, kg=kilogram, km=kilometer, lb=pound, m=meter, mbar=millibar, mm=millimeter, mm H2O=mm water at 4C, min=minute, N=Newton, psi=lb/in2, s=second
Topics for pipe network analysis:
Introduction
Equations and Methodology
Hardy Cross method
Friction losses (Darcy Weisbach and Hazen Williams)
Pressure computation
Minor losses
Applications
Built-in Fluid and Material Properties
Variables
Error Messages
References
Introduction
Our pipe network analysis calculator models steady flow of liquids or gases under pressure. It can simulate city water system pipe networks, car exhaust manifolds, long pipeline networks with different diameter pipes in series, parallel pipes, groundwater flow into a slotted well screen, soil vapor extraction well design, and more. Enter flows at nodes as positive for inflows and negative for outflows. Inflows plus outflows must sum to 0. Enter one pressure in the pipe network and all other pressures are computed. All fields must have a number, but the number can be 0. You do not need to use all the pipes or nodes for the network analysis. Enter a diameter of 0.0 if a pipe does not exist. If a node is surrounded on all sides by non-existent pipes, the node's flow must be entered as 0.0. The pipe network analysis program allows a wide variety of units. After clicking Calculate, the arrows "<--, -->, v, ^" indicate the direction of flow through each pipe in the network (to the left, right, down, or up).
Losses in pipe networks can be computed by either the Darcy-Weisbach or Hazen-Williams (HW) method, selectable by clicking on the "Roughness, e" drop-down menu. If HW is used, then the fluid must be selected as "Water, 20C (68F)".
The H,V,Re output field is scrollable using the left and right arrow keys on your keyboard. Velocity is in m/s if metric units are selected for flowrate Q, and ft/s if English units are selected for Q.
Equations and Methodology
Back to Calculator
The pipe network analysis calculation uses the steady state energy equation, Darcy Weisbach or Hazen Williams friction losses, and the Hardy Cross method to determine the flow rate in each pipe, loss in each pipe, and node pressures in the network. Minor losses (due to valves, pipe bends, etc.) in pipe networks can be accounted for by using the equivalent length of pipe method.
Hardy Cross Method (Cross, 1936; Viessman and Hammer, 1993)
The Hardy Cross method is also known as the single path adjustment method and is a relaxation method used for solving pipe networks. The flow rate in each pipe is adjusted iteratively until all equations are satisfied. The method is based on two primary physical laws:
1. The sum of pipe flows into and out of a node equals the flow entering or
leaving the pipe network through the node.
2. Hydraulic head (i.e. elevation head + pressure head, Z+P/S) is
single-valued. This means that the hydraulic head at a node is the same whether it
is computed from upstream or downstream directions in the pipe network.
Pipe flows are adjusted iteratively in the pipe network using the following equation,
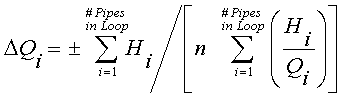
until the change in flow in each pipe is less than the convergence criteria.
n=2.0 for Darcy Weisbach losses or 1.85 for Hazen Williams losses.
Variable definitions
Friction Losses, H in Pipe Networks
Our pipe network analysis calculation gives you a choice of computing friction losses H using the Darcy-Weisbach (DW) or the Hazen-Williams (HW) method. The DW method can be used for any liquid or gas while the HW method can only be used for water at temperatures typical of municipal water supply systems. HW losses can be selected with the menu that says "Roughness, e (m):". The following equations are used:
Hazen Williams equation (Mays, 1999; Streeter et al., 1998; Viessman and Hammer, 1993) where k=0.85 for meter and seconds units or 1.318 for feet and seconds units:
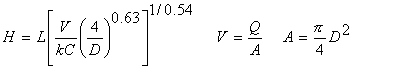
Darcy Weisbach equation (Mays, 1999; Munson et al., 1998; Streeter et al., 1998):
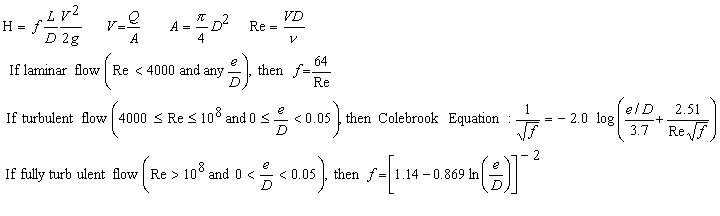
where "log" is base 10 logarithm and "ln" is natural logarithm. Variable definitions.
Pressure computation in pipe network
After computing flow rate Q in each pipe, loss H in each pipe, using the input node elevations Z and known pressure at one node, the pressure P at each node is computed around the pipe network:
Pj = S(Zi - Zj - Hpipe) + Pi where node j is down-gradient from node i. S = fluid weight density [F/L3].
Minor Losses
Minor losses such as pipe elbows, bends, and valves may be included by using the equivalent length of pipe method (Mays, 1999). Equivalent length (Leq) may be computed using the calculator which uses the formula Leq=KD/f. f is the Darcy-Weisbach friction factor for the pipe containing the fitting, and cannot be known with certainty until after the pipe network program is run. However, since you need to know f ahead of time, a reasonable value to use is f=0.02, which is the default value. We also recommend using f=0.02 even if you select Hazen-Williams losses in the pipe network analysis calculation.
For example, there is a 100-m long 10-cm diameter (inside diameter) pipe with one fully open gate valve and three regular 90o elbows. Using the equivalent length of pipe calculator, Leq is 1.0 m for the fully open gate valve and 1.25 m for each elbow. The pipe length you should enter into the pipe network analysis calculator is 100 + 1.0 + 3(1.25) = 104.75 m. The pipe network analysis calculator allows a variety of units such as m, cm, inch, and ft for diameter; and m, km, ft, and miles for equivalent length. If a fitting is not listed, select "User enters K" and enter the K value for the fitting.
Applications of Pipe Networks
The pipe network analsyis calculation has many applications. Two examples will be provided.
1. Municipal water supply system. A water tower is located at node D. The other nodes could represent industries or homes. Enter the water withdrawals at all the nodes as negative numbers, then enter the inflow to the pipe network from the water tower at node D as a positive number equal to the sum of the withdrawals from the other nodes. Usually, cities require a certain minimum pressure everywhere in the system, often 40 psi. Use the drop-down menu to select the node that you expect will have the lowest pressure in the pipe network - possibly the node furthest from D or the one at the highest elevation; we'll use node I. Enter the pressure at node I as 40 psi. Enter all the pipe lengths, diameters and node elevations. Then click "Calculate". You can use your right and left arrow keys to scroll to the left and right to see the velocity in each pipe. Typically, you want municipal water pipe velocities to be around 2 to 5 ft/s. If you are designing a pipe network (as opposed to analyzing a pipe network that is already in place), vary the pipe diameters until the pipe velocities are reasonable and pressure at node D is as low as possible to minimize the height of the water tower. There will be a trade-off between pressure at D and pipe diameters in the pipe network. Smaller diameter pipes will save money on pipes but will require a taller water tower. The water tower height is proportional to the pressure at D according to h=P/S, where P is the pressure at D. S is the weight density of the water, and h is the water tower height required. A more detailed example.
2. Manifold. A manifold has multiple inflows at various positions along the same pipeline, and one outflow. Let node I be the outflow from the pipe network and use all other nodes A-H as inflow locations; so flow is from node A through pipes 1, 2, 5, 7, 6, 8, 11, and 12 and out node I. Enter the diameters and lengths of these pipes and the desired inflows at nodes A-H. Enter the outflow at node I as a positive number equal to the sum of the inflows at nodes A-H. Enter the diameters of pipes 3, 4, 9, and 10 as 0.0 since they are non-existent pipes. Enter the elevations of all nodes. For a horizontal pipe, set all the elevations to the same value or just to 0.0 to keep it simple. From the drop-down menu, select the node where you know the pressure and enter its pressure. Clicking "Calculate" will give the flowrate in all network pipes and the pressure at all the network nodes.
Built-in Fluid and Material Properties
In the pipe network analysis calculator, the user may manually enter fluid density and viscosity or select one of the common liquids or gases from the drop-down menu. Density and viscosity for the built-in fluids were obtained from Munson et al. (1998). Likewise, the user may manually enter material roughness or Hazen-Williams C, or select one of the common pipe materials listed in the other drop-down menu. Surface roughnesses for the built-in materials were compiled from Munson et al. (1998), Streeter et al. (1998) and Mays (1999).
Variables
[ ] indicates units: F=force, L=length, P=pressure, T=time
Back to Calculator
Fluid density and viscosity may be entered in a wide choice of units. Some of the density units are mass density (g/cm3, kg/m3, slug/ft3, lb(mass)/ft3) and some are weight density (N/m3, lb(force)/ft3). There is no distinction between lb(mass)/ft3 and lb(force)/ft3 in the density since they have numerically equivalent values and all densities are internally converted to N/m3. Likewise, fluid viscosity may be entered in a wide variety of units. Some of the units are dynamic viscosity (cP, poise, N-s/m2 (same as kg/m-s), lb(force)-s/ft2 (same as slug/ft-s) and some are kinematic viscosity (cSt, stoke (same as cm2/s), ft2/s, m2/s). All viscosities are internally converted by the pipe network analysis calculator to kinematic viscosity in SI units (m2/s). If necessary, the equation Kinematic viscosity = Dynamic viscosity/Mass density is used internally.
A = Pipe area [L2].
C = Hazen Williams coefficient. Selectable as last item in drop-down menu
saying "Roughness, e".
D = Pipe diameter [L].
e = Pipe roughness [L]. All pipes must have the same roughness.
f = Moody friction factor, used in Darcy Weisbach friction loss equation.
g = Acceleration due to gravity = 32.174 ft/s2 = 9.8066 m/s2.
H = Head losses in pipe [L]. Can also be expressed in pressure units [P].
k = Constant in Hazen Williams equation for computing H.
K = Minor loss coefficient.
L = Pipe length [L].
Leq = Equivalent length of pipe for minor losses [L].
n = Constant used in Hardy Cross equation.
P = Node pressure [P]. Can also be expressed in length units [L].
Q = Flowrate through pipe, or into or out of node [L3/T]. Also
known as discharge or capacity.
Re = Reynolds number.
S = Specific Weight of Fluid (i.e. weight density; weight per unit volume) [F/L3].
Typical units are N/m3 or lb(force)/ft3. Note that
S=(mass density)(g)
V = Velocity in pipe [L/T].
Z = Elevation of node [L].
Z+P/S = Hydraulic head [L]. Also known as piezometric head. Can also
be expressed in pressure units [P].
ν = Kinematic viscosity of fluid [L2/T]. Greek letter
"nu". Note that kinematic viscosity is equivalent to dynamic (or absolute)
viscosity divided by mass density. Mass density=S/g.
Error Messages
Back to Calculator
"Node Q's must sum to 0". Check the node flow rates that you
entered. Total flow into pipe network must equal total flow out of pipe network.
"Total inflow must be >0". Check that you have positive flow
into the pipe network. You have entered all node flows as 0.0 or negative.
"Node i must have Q=0". Node i is completely surrounded by pipes
having diameters less than 0.001 m, which is the criterion the pipe network program uses for treating
pipes as being non-existent. You cannot have flow in or out of a node that is
surrounded by non-existent pipes.
"|Q| must be < 1e9 m3/s". Node flows
cannot exceed 109 m3/s. | | is absolute value.
"P at isolated node." Be sure that the "P known at node
x" drop-down menu indicates a node that is surrounded by at least one existing pipe
(i.e. a pipe having a diameter greater than 0.001 m). If you don't know the pressure
anywhere in your system, just enter 0.0 for the pressure. All the other node
pressures will be computed relative to the pressure you enter.
"Density must be > 0", "Density too high", "Viscosity must
be > 0", "Viscosity too high.". These messages can only occur
if "Another fluid" is selected from the fluid drop-down menu. Be sure the
density and viscosity you enter are greater than zero but less than 1010 kg/m3
and 1010 m2/s, respectively.
"D must be < 1e6 m". Individual pipe diameters in the pipe network cannot exceed
106 m.
"L must be < 1e7 m". Individual pipe lengths in the pipe network cannot exceed 107
m.
"|Z| must be < 1e20", " |P| must be < 1e20 m".
The absolute value of each node elevation and pressure that are input in the pipe network cannot exceed 1020
m.
"Need Water (20C) if H-W". If "Hazen-Williams C" is
selected from the Roughness drop-down menu, you must also select "Water, 20C (68F)"
from the fluid drop-down menu. The Hazen-Williams method for head losses
is only valid for water at typical city water supply temperatures, such as 20C.
"C out of range", "e out of range". These messages can
only occur if you selected "Another material" from the pipe material drop-down
menu. Valid ranges are 0<C<1000
and 0 ≤ e < 10.0 m. Normally, C
will not exceed 150 and e will not exceed 0.001 m, but we allow high ranges for those who
like to experiment.
"Pipe i e/D out of range". See the equations above for Friction loss computation using Darcy-Weisbach. e/D
cannot exceed 0.05 unless Reynolds number is less than 4000. Also, e/D cannot be 0.0
(i.e. e cannot be 0.0) if Reynolds number is greater than 108.
"Unusual input." If you experiment with the pipe network calculation long
enough, you may enter some very unusual input combinations. Some situations are
physically not possible, but the calculation will continue iterating to compute the pipe
flows and losses. After 5000 iterations (a few seconds of real time), the program
will stop running and give you this error message, so you can check your input and enter
more realistic numbers. The pipe network analysis calculator has been designed so that it will not "lock
up".
References
Back to Calculator
Cross, Hardy. Analysis of flow in networks of conduits or conductors. University of Illinois Bulletin No. 286. November 1936.
Mays, L. W. editor. 1999. Hydraulic design handbook. McGraw-Hill Book Co.
Munson, B.R., D. F. Young, and T. H. Okiishi. 1998. Fundamentals of Fluid Mechanics. John Wiley and Sons, Inc. 3ed.
Streeter, V. L., E. B. Wylie, and K. W. Bedford. 1998. Fluid Mechanics. WCB/McGraw-Hill. 9ed.
Viessman, W. and M. J. Hammer. 1993. Water Supply and Pollution Control.
HarperCollins College Publishers. 5ed.
© 2001-2025 LMNO Engineering, Research, and Software, Ltd. All rights reserved.
LMNO Engineering, Research, and Software, Ltd.
7860 Angel Ridge Rd. Athens, Ohio 45701 USA Phone: (740) 707-2614
LMNO@LMNOeng.com
https://www.LMNOeng.com
