Time of concentration calculator units: ft=foot, km=kilometer, m=meter, min=minute, s=second.
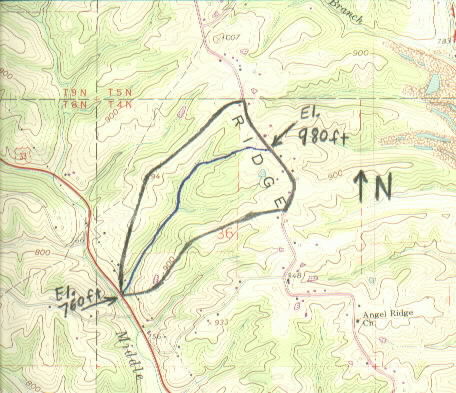
Fig. 1. Sample Watershed.
Heavy black line indicates watershed boundary
Heavy blue line indicates longest watercourse.
Length of longest watercourse = 4500 ft. (curvy length)
Slope of longest watercourse = (980-760) ft / 4500 ft = 0.0489 ft/ft = 0.0489 m/m
Introduction
Time of concentration is a fundamental watershed parameter. It is used to compute the peak
discharge for a watershed. The peak discharge is a function of the rainfall intensity,
which is based on the time of concentration. Time of concentration is the longest time
required for a particle to travel from the watershed divide to the watershed outlet. Each
of the three equations used in our time of concentration calculation require inputs for
the longest watercourse length in the watershed (L), the average slope of that watercourse
(S), and a coefficient representing the type of ground cover. Usually L and S can be
obtained from topographic maps as in Fig. 1 above. The coefficient is determined from
photographs of the watershed or field reconnaissance. Our calculation computes the time of
concentration and average velocity in the longest watercourse. A variety of units may be
selected.
Time of concentration calculator uses the FAA, Kirpich, and Kerby equations. The FAA (U.S.
Federal Aviation Administration) equation is the most commonly used of the three because
it uses the widely recognized Rational Coefficient to describe watershed ground cover. The
ASCE (American Society of Civil Engineers) recommends its use. The Kirpich equation,
developed in 1940, is the oldest of the three equations and is probably the most widely
recognized, but no longer the most commonly used. The Kerby equation is the least common
of the three equations and has the most limitations. Please see the section below for
applicability of the equations. There are other equations for time of concentration, but
most of them require rainfall intensity as an input. Thus, using those other equations to
determine the rainfall intensity for computing peak discharge results in an iterative
process because the rainfall intensity itself is a function of the time of concentration.
Equations
The following equations are used for the time of concentration calculation. All of the equations shown below use
the English units indicated in the Variables section. Of course, our calculation uses a
variety of units with all of the unit conversions handled internally by the program. The
equations can be found in Chin (2000), Chow et al. (1988), Corbitt (1999), and Singh
(1992).
FAA equation: t = G (1.1 - c) L0.5 / (100 S)1/3
Kirpich equation: t = G k (L / S0.5) 0.77
Kerby equation: t = G (L r / S0.5) 0.467
Recommendations
The FAA method was developed from data obtained from airport runoff but has been
successfully applied to overland flow in urban areas.
The Kirpich equation was developed from data obtained in seven rural watersheds in
Tennessee (USA). The watersheds had well-defined channels and steep slopes of 0.03 to 0.1
ft/ft (3 to 10%) and areas of 1 to 112 acres. It is used widely in urban areas for both
overland flow and channel flow; and it is used for agricultural watersheds up to 200 acres
(80 hectares).
The Kerby equation was developed from data obtained in watersheds having watercourses less
than 1200 ft. (365 m), slopes less than 0.01 ft/ft (1%), and areas less than 10 acres (4
hectares).
Variables
The units refer to the units that must be used in the equations shown above.
However, a variety of units may be used in our calculation.
c = Rational method runoff coefficient. See Table of Coefficients below.
G = Constant. FAA: G=1.8, Kirpich: G=0.0078, Kerby: G=0.8268
k = Kirpich adjustment factor. See Table of Coefficients below.
L = Longest watercourse length in the watershed, ft.
r = Kerby retardance roughness coefficient. See Table of Coefficients below.
S = Average slope of the watercourse, ft/ft or m/m.
t = Time of concentration, minutes.
V = Average velocity in watercourse, ft/min. V=L/t.
Table of Coefficients
| Ground Cover | Rational Runoff Coefficient for FAA Method, c (Corbitt, 1999; Singh, 1992) |
| Lawns | 0.05 - 0.35 |
| Forest | 0.05 - 0.25 |
| Cultivated land | 0.08-0.41 |
| Meadow | 0.1 - 0.5 |
| Parks, cemeteries | 0.1 - 0.25 |
| Unimproved areas | 0.1 - 0.3 |
| Pasture | 0.12 - 0.62 |
| Residential areas | 0.3 - 0.75 |
| Business areas | 0.5 - 0.95 |
| Industrial areas | 0.5 - 0.9 |
| Asphalt streets | 0.7 - 0.95 |
| Brick streets | 0.7 - 0.85 |
| Roofs | 0.75 - 0.95 |
| Concrete streets | 0.7 - 0.95 |
| Ground Cover | Kirpich Adjustment Factor, k (Chow et al., 1988; Chin, 2000) |
| General overland flow and natural grass channels | 2.0 |
| Overland flow on bare soil or roadside ditches | 1.0 |
| Overland flow on concrete or asphalt surfaces | 0.4 |
| Flow in concrete channels | 0.2 |
| Ground Cover | Kerby Retardance Coefficient, r (Chin, 2000) |
| Conifer timberland, dense grass | 0.80 |
| Deciduous timberland | 0.60 |
| Average grass | 0.40 |
| Poor grass, bare sod | 0.30 |
| Smooth bare packed soil, free of stones | 0.10 |
| Smooth pavements | 0.02 |
Error Messages given by calculation
"Need S>0", "Need L>0". Initial input checks.
Slope and Length must be positive numbers.
"Need 0<c≤1 for FAA". c must be in this range for the FAA equation.
"Need k>0 for Kirpich", "Need r>0 for Kerby". Input checks.
References
Chin, David A. 2000. Water-Resources Engineering. Prentice-Hall.
Chow, Ven Te, David R. Maidment, and Larry W. Mays. 1988. Applied Hydrology. McGraw-Hill.
Corbitt, Robert A. 1999. Standard Handbook of Environmental Engineering. McGraw-Hill. 2ed.
Singh, Vijay P. 1992. Elementary Hydrology. Prentice-Hall.
© 2003-2026 LMNO Engineering, Research, and Software, Ltd. (All Rights Reserved)
LMNO Engineering, Research, and Software, Ltd.
7860 Angel Ridge Rd. Athens, Ohio 45701 USA Phone: (740) 707-2614
LMNO@LMNOeng.com
https://www.LMNOeng.com
