Units: cm=centimeter, cfs=cubic foot per second, ft=foot, gal=gallon (U.S.), hr=hour, km=kilometer, m=meter, min=minute, s=second, yr=year

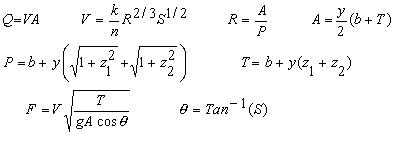
Topics: Introduction Variables Manning n coefficients Error Messages References
Introduction
Many natural and man-made channels are approximately trapezoidal. Our trapezoidal open channel calculator uses the most commonly used equation for analyzing rivers and streams - the Manning equation. It is the equation beginning with V=... above. The Manning equation is best used for uniform steady state flows. Uniform means that the cross-section geometry of the channel remains constant along the length of the channel, and steady state means that the velocity, discharge, and depth do not change with time. Though these assumptions are rarely ever strictly achieved in rivers and streams, the Manning equation is still used to model most rivers and streams where conditions are relatively steady and for reaches (portions of rivers) that have a reasonably constant cross-section for a long enough distance that the depth remains fairly constant.
The Manning equation is a semi-empirical equation. Thus, its units are inconsistent. The factor, k, has units which allow the equation to be used properly. Our calculator takes care of all the unit conversions for you, and allows you to enter and compute variables in a wide variety of units.
In our trapezoidal open channel calculator, most of the combinations of inputs have analytic (closed form) solutions to compute the unknown variables; however, some combinations of inputs require numerical solution. Our numerical solutions utilize a cubic solver that finds roots of the equations with the result accurate generally to at least 8 significant digits. All of our calculations utilize double precision. Two depths and bottom widths are possible for certain combinations of entered values when Q, T, n, and S or V, T, n, and S are entered. Since two solutions are possible for some input combinations, the text fields are extra wide to accommodate two numbers.
Variable Definitions
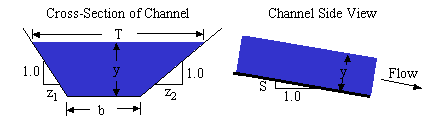
[ ] indicates dimensions. [L]=Length, [T]=Time.
To calculator
A = Flow cross-sectional area, determined normal (perpendicular) to the bottom surface [L2].
b = Channel bottom width [L].
F = Froude number. F is a non-dimensional parameter indicating the
relative effect of inertial effects to gravity effects. River flows with F<1
are low velocity flows called subcritical. F>1 are high velocity flows
called supercritical. Subcritical flows are controlled by downstream obstructions
while supercritical flows are affected by upstream controls. F=1 flows are
called critical.
g = acceleration due to gravity = 32.174 ft/s2 = 9.8066 m/s2.
g is used in the equation for Froude number.
k = unit conversion factor = 1.49 if English units = 1.0 if metric units.
Our software converts all inputs to SI units (meters and seconds), performs the
computations using k=1.0, then converts the computed quantities to units
specified by the user.
n = Manning coefficient. n is a function of the channel material,
such as grass, concrete, earth, etc. Values for n can be found in the table
of Manning's n coefficients shown below.
P = Wetted perimeter [L]. P is the contact length between the
water and the channel bottom and sides.
Q = Discharge or flow rate [L3/T].
R = Hydraulic radius of the flow cross-section [L].
S = Slope of channel bottom or water surface [L/L]. Vertical distance
divided by horizontal distance.
T = Top width of the flowing water [L].
V = Average velocity of the water [L/T].
y = Water depth measured normal (perpendicular) to the bottom of the channel
[L]. If the channel has a small slope (S), then using the vertical depth
introduces only minimal error.
z1, z2 = Side slopes of each bank of the channel.
These slopes are computed as horizontal distance divided by vertical distance.
θ = Angle formed by S.
Manning's n Coefficients
To calculator
The Manning's n coefficients were compiled from the references listed under Discussion and References and in the references at the bottom of this web page (note the footnotes which refer to specific references).
| Material | Manning n | Material | Manning n |
| Natural Streams | Excavated Earth Channels | ||
| Clean and Straight | 0.030 | Clean | 0.022 |
| Major Rivers | 0.035 | Gravelly | 0.025 |
| Sluggish with Deep Pools | 0.040 | Weedy | 0.030 |
| Stony, Cobbles | 0.035 | ||
| Metals | Floodplains | ||
| Brass | 0.011 | Pasture, Farmland | 0.035 |
| Cast Iron | 0.013 | Light Brush | 0.050 |
| Smooth Steel | 0.012 | Heavy Brush | 0.075 |
| Corrugated Metal | 0.022 | Trees | 0.15 |
| Non-Metals | |||
| Glass | 0.010 | Finished Concrete | 0.012 |
| Clay Tile | 0.014 | Unfinished Concrete | 0.014 |
| Brickwork | 0.015 | Gravel | 0.029 |
| Asphalt | 0.016 | Earth | 0.025 |
| Masonry | 0.025 | Planed Wood | 0.012 |
| Unplaned Wood | 0.013 | ||
| Corrugated Polyethylene (PE) with smooth inner walls a,b | 0.009-0.015 | ||
| Corrugated Polyethylene (PE) with corrugated inner walls c | 0.018-0.025 | ||
| Polyvinyl Chloride (PVC) with smooth inner walls d,e | 0.009-0.011 | ||
Error Messages
To calculator
"Invalid boxes checked." This message is displayed if too many or too few variables are selected to be entered. A problem cannot be over-stated or under-stated. In all, there are 30 combinations of inputs which are acceptable. This message can be displayed to both registered and non-registered users.
"Cannot be computed." This message is displayed in numeric fields if enough variables are selected to compute some values but not others. For instance, if only Q, y, and b are input, then n, S, and F cannot be computed but other values will be computed.
The following messages are displayed if an entered value lies outside the acceptable
range for the variable. These messages are only displayed when the
"Calculate" button is clicked - for registered users.
"b must be > 0", "b must be 1e-9 to 10000 m", "n must be
1e-9 to 100", "Q must be > 0", "Q must be 1e-9 to 1e9 m3/s",
"S must be 1e-9 to 1e9", "T must be > 0", "T must be 1e-9 to
10000 m", "V must be > 0", "V must be 1e-9 to 1e9 m/s",
"y must be < 0", "y must be 1e-9 to 1e9 m", "z1, z2
must be ≥ 0", "z1, z2 cannot both be 0".
Note that the channel cannot have both z1=0 and z2=0. However,
if you wish to simulate a rectangular channel, you can set one of them to 0.0 and the
other to a very small positive number such as 0.00001. Or, you can use our rectangular open channel calculator. Triangular channels
can be modeled by setting the bottom width, b, to a very small positive number such as
0.001 m or as low as 10-9 m.
The following messages are displayed if the values entered result in an infeasible
situation. For instance, entering certain combinations of values for T, Q, n,
and S can result in an impossible flow situation indicated by a negative bottom
width or negative depth. These messages are only displayed when the
"Calculate" button is clicked - for registered users.
"b will be < 0","T will be > 10000 m", "y will be
< 0", "y will be ≤ 0", "y or b will be < 0".
The calculator uses an upper limit of 10,000 m for top width.
References
To calculator
A further discussion of open channel flow, Manning's equation, and trapezoidal channel geometry can be found in these references and on our discussion page. The Manning's n coefficients shown above are compiled from the references shown here. The footnotes refer to specific values shown in the Manning n table above.
a Barfuss, Steven and J. Paul Tullis. Friction factor test on high density polyethylene pipe. Hydraulics Report No. 208. Utah Water Research Laboratory, Utah State University. Logan, Utah. 1988.
c Barfuss, Steven and J. Paul Tullis. Friction factor test on high density polyethylene pipe. Hydraulics Report No. 208. Utah Water Research Laboratory, Utah State University. Logan, Utah. 1994.
e Bishop, R.R. and R.W. Jeppson. Hydraulic characteristics of PVC sewer pipe in sanitary sewers. Utah State University. Logan, Utah. September 1975.
Chaudhry, M. H. 1993. Open Channel Flow. Prentice-Hall, Inc.
Chow, V. T. 1959. Open Channel Hydraulics. McGraw-Hill, Inc. (the classic text)
French, R. H. 1985. Open Channel Hydraulics. McGraw-Hill Book Co.
Mays, L. W. editor. 1999. Hydraulic design handbook. McGraw-Hill Book Co.
Munson, B.R., D. F. Young, and T. H. Okiishi. 1998. Fundamentals of Fluid Mechanics. John Wiley and Sons, Inc. 3ed.
d Neale, L.C. and R.E. Price. Flow characteristics of PVC sewer pipe. Journal of the Sanitary Engineering Division, Div. Proc 90SA3, ASCE. pp. 109-129. 1964.
Streeter, V. L., E. B. Wylie, and K. W. Bedford. 1998. WCB/McGraw-Hill. 9ed.
b Tullis, J. Paul, R.K. Watkins, and S. L. Barfuss. Innovative new drainage pipe. Proceedings of the International Conference on Pipeline Design and Installation, ASCE. March 25-27, 1990.
© 2000-2026 LMNO Engineering, Research, and Software, Ltd. All rights reserved.
LMNO Engineering, Research, and Software, Ltd.
7860 Angel Ridge Rd. Athens, Ohio 45701 USA Phone: (740) 707-2614
LMNO@LMNOeng.com
https://www.LMNOeng.com
