LMNO Engineering logo LMNO Engineering, Research, and Software, Ltd.

Critical Depth

Critical depth in circular pipe (culvert) is a function of the flow rate and pipe diameter

Register to enable "Calculate" button.

Diameter, D: 
Flowrate, Q: 
Critical Depth, Yc:    inch
www.​LMNOeng.com
© LMNO Engineering, Research, and Software, Ltd.


Units in critical depth calculation: cm=centimeter, ft=feet, gal=US gallons, m=meters, min=minute, s=second


Introduction

For water flowing in a culvert, it is important to know the critical depth. Though water may not actually be flowing at the critical depth, it is helpful to know if the actual water depth is greater than or less than critical. Critical depth is a quantity of fundamental importance to understanding the flow characteristics. If the actual depth is greater than critical depth, then the flow is considered "subcritical". Subcritical flow is "slow flow" and is impacted by downstream conditions. If the actual depth is less than critical depth, then the flow is "supercritical". Supercritical flow is "fast flow" and is impacted by upstream conditions. It flows faster than the wave speed and is unimpacted by downstream conditions. A detailed discussion of subcritical and supercritical flow can be found on our gradually varied flow calculation page.

As water flows down a culvert, the depth may change and pass through the critical depth if the bottom slope, geometry, or pipe material changes. If the flow is initially subcritical and the channel slope increases, the water may undergo a hydraulic drop if it transitions from subcritical to supercritical. Conversely, if the flow is supercritical and the culvert slope becomes flatter, then there could be a hydraulic jump such that the water passes through the critical depth as it becomes subcritical.


Equations

For a circular pipe, critical depth can be computed based on first principles (mass, momentum, and energy conservation). For a mild downward sloping culvert (slope less than about 10%), the specific energy is (Chow, 1959, p. 41):

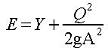
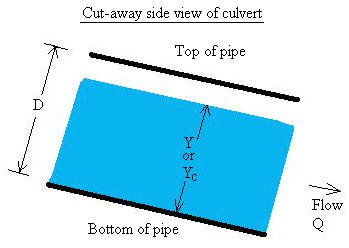
Specific energy equation    Side view of culvert


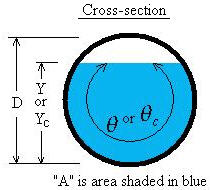
The channel cross-sectional area can be written in terms of the geometry as (Chow, 1959, p. 21):

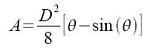
Area equation    Cross-section of pipe


Critical depth occurs when energy is at a minimum with respect to depth, dE/dY=0. The following equation is obtained when energy is minimized:

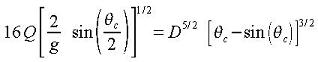
Critical depth equation


LMNO Engineering uses a numerical solution method to solve the above equation for θc and then for Yc.

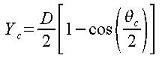
Critical depth equation


Notation

Our calculation allows you to use a variety of units with all of the conversions computed internally. The units shown below are SI (international system of units).
A = Flow area of water, m2.
D = Inside diameter of pipe (culvert), m.
E = Specific energy, m.
g = Acceleration of gravity = 9.8066 m/s2.
Q = Flow rate (discharge), m3/s.
V = Velocity, m/s.
Y = Water depth, m.
Yc = Critical depth, m.
θ = Angle of water in cross-section, radians.
θc = Angle at critical depth, radians.


Messages given by calculation

"Need Diameter > 0", "Need Flowrate > 0", "Need D≥1e-6 m", "Need D≤1000 m", "Need Q≥1e-9 m3/s", "Need Q≤1e6 m3/s". These are input checks. Input diameter and flow rate must be positive numbers. D must be between 10-6 m and 1000 m. Q must be between 10-9 m3/s and 106 m3/s.

"Need larger Q or smaller D". Run-time error. The combination of flow rate and diameter that were input result in a very small critical depth approaching machine precision.

"Need smaller Q or larger D". Run-time error. The combination of flow rate and diameter that were input result in critical depth greater than the pipe diameter.


Reference

Chow, V. T. 1959. Open-Channel Hydraulics. McGraw-Hill, Inc.

© 2009-2025 LMNO Engineering, Research, and Software, Ltd.  All rights reserved.

LMNO Engineering, Research, and Software, Ltd.
7860 Angel Ridge Rd.   Athens, Ohio  45701   USA   Phone: (740) 707-2614
LMNO@LMNOeng.com    https://www.LMNOeng.com